Παράδοξο χαρακτηρίζεται οτιδήποτε που αντιβαίνει στη κοινή αντίληψη, ή κάτι που συμβαίνει και θεωρείται απίστευτο.

Ως ουσιαστικό σημαίνει οτιδήποτε προκαλεί έκπληξη. Η έννοια του παράδοξου εξετάζεται τόσο από φιλοσοφική και φιλολογική ερμηνεία όσο και από επιστημονική έρευνα. Στη φιλοσοφική και επιστημονική σκέψη το πραγματικό παράδοξο εκθέτει τα λάθη μας στην κατανόηση μιας κατάστασης εκ της οποίας προκύπτουν στο τέλος τα λογικά αδιέξοδα σε επιμέρους ζητήματα (παράδοξα), η έννοια παραπέμπει ετυμολογικά στην αιτία του λογικού αδιεξόδου που είναι η θεμελιακά λάθος κατανόηση μιας κατάστασης η οποία γεννά τελικά το λογικό αδιέξοδο.

 

ΠΑΡΑΔΕΙΓΜΑΤΑ ΠΑΡΑΔΟΞΩΝ

 

Παράδοξο του Επιμενίδη

Κρῆτες ἀεὶ ψεῦσται (οι Κρήτες είναι πάντα ψεύτες)
Σύμφωνα λοιπόν με την έκφραση αυτοί όλοι οι Κρήτες είναι ψεύτες. Ωστόσο ποιος θα μπορούσε να βασιστεί σε αυτά τα λόγια του – επίσης καταγόμενου από την Κρήτη – Επιμενίδη; Εκεί ακριβώς έγκειται το παράδοξο: αν βασιστούμε στην παραπάνω πρόταση τότε και ο ίδιος ο Επιμενίδης ψεύδεται, άρα τελικά οι Κρήτες δεν είναι ψεύτες. Τότε όμως κι ο Επιμενίδης δεν ψεύδεται.

 

Παράδοξα του Ζήνωνα

Αχιλλέας και η χελώνα
Στο παράδοξο του Αχιλλέα και της χελώνας ο Αχιλλέας είναι σε αγώνα δρόμου με μια χελώνα. ο Αχιλλέας επιτρέπει στη χελώνα ένα προβάδισμα 100 μέτρων. Για παράδειγμα, αν υποθέσουμε ότι οι 2 δρομείς θα τρέχουν με σταθερή ταχύτητα μετά από πεπερασμένο χρόνο ο Αχιλλέας θα έχει τρέξει 100 μετρά και θα έχει φτάσει το σημείο εκκίνησης της χελώνας. Κατά τη διάρκεια αυτού του χρόνου η χελώνα θα έχει διανύσει πολύ μικρότερη απόσταση (π.χ 10 μέτρα). Στη συνέχεια, θα πάρει τον Αχιλλέα λίγο περισσότερο χρόνο για να τρέξει την απόσταση, στον οποίο η χελώνα θα έχει προχωρήσει πιο μακριά και στη συνέχεια περισσότερο χρόνο ακόμα για να φτάσει αυτό το τρίτο σημείο, ενώ η χελώνα κινείται μπροστά. Έτσι, κάθε φορά που ο Αχιλλέας φτάνει κάπου η χελώνα έχει πάει ακόμα πιο μακριά. Ως εκ τούτου, επειδή υπάρχει ένας άπειρος αριθμός των σημείων που ο Αχιλλέας πρέπει να φθάσει και η χελώνα έχει ήδη πάει, δεν μπορεί ποτέ να ξεπεράσει τη χελώνα.

 

Το παράδοξο του βέλους
Στο παράδοξο του βέλους, ο Ζήνων ισχυρίζεται ότι για να υπάρξει κίνηση, ένα αντικείμενο πρέπει να αλλάξει τη θέση που κατέχει. Δίνει ένα παράδειγμα ενός βέλους κατά την πτήση. Δηλώνει ότι σε κάθε μία χρονική στιγμή, το βέλος ούτε κινείται προς όπου είναι, ούτε όπου δεν είναι. Δεν μπορεί να κινηθεί προς όπου δεν είναι, γιατί δεν υπάρχει χρόνος που μεσολαβεί για να μετακινηθεί εκεί. Δεν μπορεί να κινηθεί προς όπου είναι, γιατί είναι ήδη εκεί. Με άλλα λόγια, σε κάθε χρονική στιγμή δεν υπάρχει καμία κίνηση. Αν όλα είναι ακίνητα σε κάθε στιγμή, και ο χρόνος αποτελείται εξ ολοκλήρου από στιγμές, τότε η κίνηση είναι αδύνατη.

 

Το παράδοξο του Χίλμπερτ

Η Αλγεβρα Boole (Boolean algebra) πήρε το όνομά της από τον G. Boole (1815-1864), ο οποίος ανέπτυξε ένα αλγεβρικό σύστημα (1854) για τη συστηματική αντιμετώπιση της λογικής. Τα αξιώματα της Αλγεβρας Boole διατυπώθηκαν από τον E. V. Huntington (1904).

Οι μεταβλητές που χρησιμοποιούνται στην Αλγεβρα Boole ονομάζονται λογικές μεταβλητές γιατί μπορούν να πάρουν δύο (2) μόνο τιμές: 0 και 1. Αυτός είναι ο λόγος που η Αλγεβρα Boole αποτελεί τη βάση για τα ψηφιακά ηλεκτρονικά κυκλώματα.

Στην Αλγεβρα Boole ορίζονται τρεις βασικές πράξεις:

α)     η πράξη NOT (ΟΧΙ) με σύμβολο – (π.χ. à ) και διαβάζεται συμπλήρωμα Α

β)     η πράξη AND (ΚΑΙ) με σύμβολο ·

γ)     η πράξη OR (Η) με σύμβολο +

Ωστόσο το 1938 ο C. Shannon έδειξε ότι η Άλγεβρα Boole μπορούσε να εφαρμοστεί στην απλοποίηση και στη σχεδίαση των ηλεκτρονικών κυκλωμάτων, όπως, για παράδειγμα στα τηλεφωνικά κυκλώματα. Αργότερα χρησιμοποιήθηκε για τη σχεδίαση των κυκλωμάτων των υπολογιστών.

Τα ηλεκτρονικά κυκλώματα που εκτελούν τις βασικές πράξεις της Άλγεβρας Boole καλούνται λογικές πύλες. Κάθε τέτοια πύλη δέχεται στην είσοδό της σήματα με τη μορφή υψηλής ή χαμηλής ηλεκτρικής τάσης και δίνει στην έξοδό της ένα μοναδικό λογικό αποτέλεσμα με τη μορφή υψηλής ή χαμηλής ηλεκτρικής τάσης. Συνδυάζοντας κατάλληλα λογικές πύλες δημιουργούνται πιο σύνθετα κυκλώματα που μπορούν να εκτελούν λογικές πράξεις.

Αρχικά για την υλοποίηση των λογικών πυλών χρησιμοποιήθηκαν διακριτά ηλεκτρονικά στοιχεία. Σήμερα στα ολοκληρωμένα κυκλώματα υπάρχει ένα μεγάλο πλήθος επιμέρους κυκλωμάτων, τα οποία με τη σειρά τους αποτελούνται από πλήθος λογικών πυλών.

Οι λογικές πύλες είναι τα βασικά δομικά στοιχεία στα ψηφιακά κυκλώματα. Όπως έχουμε στις οικοδομές τα τούβλα και με αυτά κατασκευάζουμε τοίχους και σύνθετες κατασκευές χρησιμοποιώντας παρόμοια υλικά ξανά και ξανά, έτσι και στα ψηφιακά κυκλώματα χρησιμοποιούμε τις λογικές πύλες για να κατασκευάσουμε σύνθετα κυκλώματα.

ΒΑΣΙΚΕΣ ΛΟΓΙΚΕΣ ΠΥΛΕΣ

 

Βασικές λογικές πύλες είναι οι:

• ΟΧΙ (NOT)
• ΚΑΙ (AND)
• Ή (OR)
• Αποκλειστικό Ή (XOR)
• ΟΧΙ-ΚΑΙ (NAND)
• ΟΧΙ – Ή (NOR)

 

Πύλη NOT

Η πύλη NOT (ΟΧΙ) έχει μόνο μία είσοδο και δίνει μόνο μία έξοδο. Η λειτουργία της είναι η αντιστροφή του λογικού σήματος της εισόδου.

Ο πίνακας αληθείας της πύλης είναι:

Είσοδος	Έξοδος
A	ΟΧΙ A
0	1
1	0

Το κυκλωματικό σχεδιάγραμμα είναι το εξής:

Πύλη AND

Η πύλη AND εκτελεί την λογική πράξη AND (ΚΑΙ) μεταξύ των εισόδων της. Η πράξη AND στην άλγεβρα Boole συμβολίζεται με επί (*). Για παράδειγμα εαν η πύλη έχει 2 εισόδους (a και b) και μία έξοδο (c) θα γίνει η πράξη:

 

Ο πίνακας αληθείας της λογικής πύλης AND φαίνεται στο εξής σχήμα:

Είσοδοι		Έξοδος
A	B	A ΚΑΙ B
0	0	0
0	1	0
1	0	0
1	1	1

 

Το κυκλωματικό σχήμα της AND 2 εισόδων είναι το εξής:

Παράδειγμα: έστω ότι a=1 και b=0. Η έξοδος c θα προκύψει 0.

Γενικότερα, η έξοδος AND δίνει λογική έξοδο 1 όταν όλες οι είσοδοί της βρίσκονται σε λογική κατάσταση 1.

Οι πύλες AND κατασκευάζονται και με περισσότερες των δύο εισόδων (πχ 3,4,5,8 είσοδοι).

 

Πύλη OR

 

Η πύλη OR εκτελεί την λογική πράξη OR (Η΄) μεταξύ των εισόδων της. Η πράξη OR στην άλγεβρα Boole συμβολίζεται με το συν (+). Για παράδειγμα εαν η πύλη έχει 2 εισόδους (a και b) και μία έξοδο (c) θα γίνει η πράξη:

 

Ο πίνακας αληθείας της λογικής πύλης OR φαίνεται στο εξής σχήμα:

Είσοδοι		Έξοδος
A	B	A Η” B
0	0	0
0	1	1
1	0	1
1	1	1

 

Το κυκλωματικό σχήμα της OR 2 εισόδων είναι το εξής:

Παράδειγμα: Έστω ότι a=1 και b=0. Η έξοδος c θα προκύψει 1.

Γενικότερα, η πύλη OR δίνει λογικό 1 όταν μία τουλάχιστο είσοδος είναι σε λογικό 1.

Οι πύλες OR κατασκευάζονται και με περισσότερες των δύο εισόδων (πχ 3,4,5,8 είσοδοι).

 

Πύλη XOR

Η πύλη XOR εκτελεί την λογική πράξη XOR (ΑΠΟΚΛΕΙΣΤΙΚΟ Η’) μεταξύ των εισόδων της. Η πράξη XOR στην άλγεβρα Boole συμβολίζεται με ένα συν μέσα σε ένα κύκλο (⊕).Για παράδειγμα εαν η πύλη έχει 2 εισόδους (a και b) και μία έξοδο (c) θα γίνει η πράξη:

 

Ο πίνακας αληθείας της λογικής πύλης ΧOR φαίνεται στο εξής σχήμα:

Είσοδοι		Έξοδος
A	B	A XOR B
0	0	0
0	1	1
1	0	1
1	1	0

 

Το κυκλωματικό σχήμα της XOR 2 εισόδων είναι το εξής:

Παράδειγμα: Έστω ότι a=1 και b=0. Η έξοδος c θα προκύψει 1.

Γενικά η πύλη XOR ελέγχει την περιττή ισοτιμία, δηλαδή δίνει λογικό 1 όταν περριτός αριθμός εισόδων βρίσκεται σε λογικό 1.

 

Πύλη NAND

Η πύλη NAND (ΟΧΙ-ΚΑΙ) δίνει την αντίθετη έξοδο από την AND, δηλαδή δίνει λογικό 1 όταν υπάρχει τουλάχιστο ένα λογικό 0 στις εισόδους.

 

Ο πίνακας καταστάσεων και το κυκλωματικό σχεδιάγραμμα είναι τα εξής:

Είσοδοι		Έξοδος
A	B	A NAND B
0	0	1
0	1	1
1	0	1
1	1	0

 

Πύλη NOR

Η πύλη NΟR (ΟΧΙ-Η’) δίνει την αντίθετη έξοδο από την OR, δηλαδή δίνει λογικό 1 όταν και οι δύο είσοδοι είναι 0. Ο πίνακας καταστάσεων και το κυκλωματικό σχεδιάγραμμα είναι τα εξής:

Είσοδοι		Έξοδος
A	B	A NOR B
0	0	1
0	1	0
1	0	0
1	1	0

 

Πύλη ΧNOR

Η πύλη ΧNΟR δίνει την αντίθετη έξοδο από την ΧOR, δηλαδή δίνει λογικό 1 όταν οι δύο είσοδοι είναι στην ίδια λογική στάθμη. Ο πίνακας καταστάσεων και το κυκλωματικό σχεδιάγραμμα είναι τα εξής:

Είσοδοι		Έξοδος
A	B	A XNOR B
0	0	1
0	1	0
1	0	0
1	1	1

ΠΙΝΑΚΑΣ :

Δοκιμάστε και μόνοι σας

Μπορείτε να δοκιμάστε και μόνοι σας τις λογικές πύλες στους παρακάτω συνδέσμους:

http://logic.ly/demo/

http://www.neuroproductions.be/logic-lab/

 

ΒΙΝΤΕΟ :

https://www.youtube.com/watch?v=iqy71uVFsnk

 

ΠΗΓΕΣ :

 

• http://ebooks.edu.gr/modules/ebook/show.php/DSGL-C127/577/3739,16398/
• https://el.wikipedia.org/wiki/%CE%9B%CE%BF%CE%B3%CE%B9%CE%BA%CE%AE_%CF%80%CF%8D%CE%BB%CE%B7
• http://users.sch.gr/kgiannaras/mathimata/psifiaka-ilektronika/logikes-pyles-kai-pinakes-alitheias.html

 

Το κυκλωματικό σχεδιάγραμμα είναι το εξής:

Ο μαθηματικός Τζορτζ Μπουλ (George Boole, 1815-1864) παρουσίασε το 1847 μια άλγεβρα με μεταβλητές δύο τιμών, το 0 και το 1 (που καλούνται «λογικές μεταβλητές»). Ουσιαστικά παρουσίασε με τα μαθηματικά της εποχής του την Αριστοτέλεια λογική του είναι ή δεν είναι. Σήμερα η άλγεβρα αυτή ονομάζεται άλγεβρα Μπουλ, ή δυαδική άλγεβρα, ή διακοπτική άλγεβρα και έχει βρει ευρεία εφαρμογή στην σχεδίαση του λογισμικού και των κυκλωμάτων των ηλεκτρονικών υπολογιστών, επειδή είναι ιδανική για χειρισμό λογικών συναρτήσεων και πράξεων στο δυαδικό σύστημα.

Σε αντίθεση με την στοιχειώδη άλγεβρα όπου οι τιμές των μεταβλητών είναι αριθμοί και οι κύριες πράξεις,που είναι η πρόσθεση και ο πολλαπλασιασμός, στην άλγεβρα Μπουλ υπάρχουν τρεις κύριες πράξεις: η σύζευξη και (συμβ. ∧), η διάζευξη ή (συμβ. ∨) και η άρνηση όχι (σύμβ. ¬).

Λογική πρόταση είναι κάθε σύνολο χαρακτήρων ή λέξεων που μπορούμε να του δώσουμε την τιμή «ψευδής» ή «αληθής». Άρα η πρόταση p=[Θα κερδίσω το λαχείο μεθαύριο] δεν είναι λογική πρόταση. Όμως η πρόταση q=[Ο ακέραιος αριθμός 4 είναι άρτιος] είναι λογική πρόταση και έχει αληθοτιμή = «αληθής». Έτσι θα μπορούσαμε να δούμε την προτασιακή λογική (πράξεις με λογικές προτάσεις) ως μια άλγεβρα Μπουλ. Ας δούμε τις αντιστοιχίες:

• Τα στοιχεία του Κ στην προτασιακή λογική είναι λογικές προτάσεις.
• Η πρόσθεση αντιστοιχεί σε διάζευξη (Ή).
• Ο πολλαπλασιασμός αντιστοιχεί σε σύζευξη (ΚΑΙ).
• Το μηδέν αντιστοιχεί στο ψευδής.
• Το ένα αντιστοιχεί στο αληθής.
• Το συμπλήρωμα αντιστοιχεί στην άρνηση της πρότασης(α’), όπου «α» ένα στοιχείο.

Η άλγεβρα μπουλ είναι μία αλγεβρική δομή ορισμένη πάνω σε ένα σύνολο στοιχείων Β με δύο πράξεις, το + και το *.

Παραδείγματως χάρη: έστω Β={0,1} και οι εσωτερικές πράξεις «+» και «*» που ορίζονται ως εξής:

x	y	x + y	x * y
1	1	1	1
1	0	1	0
0	1	1	0

 

Η άλγεβρα Μπουλ είναι θεμελιώδους σημασίας για την επιστήμη της Πληροφορικής και αποτελεί την βάση για την θεωρητική μελέτη του πεδίου της λογικής σχεδίασης. Επιπλέον είναι σημαντική σε άλλα πεδία όπως η Στατιστική, η Θεωρία συνόλων και ο προγραμματισμός.

Η Λογική είναι η μελέτη τρόπων συλλογισμού, καθώς και η χρήση έγκυρων συλλογισμών. Η λογική χρησιμοποιείται σε πολλές επιστήμες, όπως στη Φιλοσοφία, στα Μαθηματικά και στην Πληροφορική. Εξετάζει γενικές μορφές οι οποίες μπορούν να επιχειρηματολογηθούν. Στα μαθηματικά είναι η μελέτη των έγκυρων συμπερασμάτων μέσα σε μια τυπική γλώσσα. Η λογική επιπλέον μελετήθηκε στη θεωρία επιχειρηματολογίας.

Η λογική αναπτύχθηκε σε πολλούς αρχαίους πολιτισμούς, όπως σε Ινδία, Κίνα, Περσία και Ελλάδα. Η μελέτης της λογικής ήταν επίσης μέρος της γραμματικής και της ρητορικής. Στη Δύση, η λογική καθιερώθηκε ως επίσημος κλάδος από τον Αριστοτέλη, ο οποίος της έδωσε θεμελιώδη θέση στη φιλοσοφία.

Η λογική του Αριστοτέλη, και ιδιαίτερα η θεωρία του για τον συλλογισμό, είχε τεράστια επιρροή στη δυτική σκέψη. Τα έργα λογικής, που ονομάζονται ως σύνολο Το Όργανον, είναι η πρώτη τυπική μελέτη της λογικής που έχει βρεθεί. Αν και είναι δύσκολο να προσδιορίσουμε τις ημερομηνίες, η πιθανή σειρά της γραφής των λογικών έργων του Αριστοτέλη είναι:

1. Κατηγορίες, μια μελέτη για τις δέκα κατηγορίες που χαρακτηρίζουν τα όντα του αισθητού κόσμο.
2. Τοπικά (με ένα παράρτημα του που ονομάζεται Περί των Σοφιστικών ελέγχων), μια συζήτηση της διαλεκτικής,
3. Περί ερμηνείας, μια ανάλυση απλών κατηγορηματικών προτάσεων, σε απλούς όρους, άρνηση, και ενδείξεις ποσότητας, καθώς και μια ολοκληρωμένη αντιμετώπιση των εννοιών της αντίθεσης και μετατροπής. Το 7ο κεφάλαιο είναι η προέλευση του «τετραγώνου αντίθεσης» (ή λογικού τετραγώνου). Το 9ο κεφάλαιο περιέχει τις απαρχές της τροπικής λογικής.
4. Αναλυτικά Πρότερα, μια τυπική ανάλυση του έγκυρου επιχειρήματος ή «συλλογισμού».
5. Αναλυτικά Ύστερα, μια μελέτη της επιστημονικής απόδειξης, που περιέχει τις ώριμες απόψεις του Αριστοτέλη στη λογική.

Τα έργα αυτά είναι εξαιρετικής σημασίας για την ιστορία της λογικής. Ο Αριστοτέλης ήταν ο πρώτος επιστήμονας της λογικής που επιχείρησε μια συστηματική ανάλυση της λογικής σύνταξης, σε ουσιαστικό και ρήμα. Στις Κατηγορίες παρουσίασε όλα τα πράγματα, στα οποία ένα ουσιαστικό μπορεί να αναφέρεται. Αυτή η ιδέα αποτελεί τη βάση του φιλοσοφικού του έργου, τα Μεταφυσικά, τα οποία είχαν επίσης βαθιά επίδραση στη Δυτική σκέψη. Υπήρξε ο πρώτος επιστήμονας της τυπικής λογικής (δηλαδή έδωσε τις αρχές της συλλογιστικής που χρησιμοποιεί μεταβλητές για να δείξει την υποκείμενη λογική μορφή των επιχειρημάτων). Ερευνούσε τις σχέσεις εξάρτησης που χαρακτηρίζουν αναγκαστικά το συμπέρασμα, και διέκρινε την εγκυρότητα αυτών των σχέσεων, από την αλήθεια των προκείμενων (η αξιοπιστία του επιχειρήματος). Τα Αναλυτικά Πρότερα αποτελούν το εγχειρίδιο της συλλογιστικής, όπου τρεις σημαντικές αρχές εφαρμόστηκαν για πρώτη φορά στην ιστορία: η χρήση των μεταβλητών, μια καθαρά τυπική αντιμετώπιση και η χρήση ενός αξιωματικού συστήματος. Στα Τοπικά και Περί των Σοφιστικών ελέγχων ανέπτυξε επίσης μια θεωρία μη-τυπικής λογικής (π.χ. θεωρία των πλανών.)

Κατερίνα Β. & Σταμάτης Β.

Είναι γνωστό σε όλους ότι οι Θεωρητικές και οι Θετικές Επιστήμες έχουν αμέτρητα πράγματα να «χωρίσουν». Γι’ αυτόν τον λόγο κάθε μαθητής Λυκείου βρίσκεται σε δύσκολη θέση, όταν καλείται να κάνει αυτή την ξεχωριστή επιλογή μεταξύ των Αρχαίων, της Φιλοσοφίας, της Ιστορίας και των Μαθηματικών, της Φυσικής, της Χημείας…..

Σίγουρα τα Μαθηματικά και η Φιλοσοφία είναι δύο διαφορετικές επιστήμες κυρίως στην εποχή μας, όπου κάθε επιστήμη προσπαθεί να εξειδικεύεται . Γι’ αυτό άλλωστε η βαθιά και σημαντική σχέση που υπάρχει ανάμεσα στα Μαθηματικά και τη Φιλοσοφία έχει αποδυναμωθεί.

Σ’ αυτό σίγουρα έχει βοηθήσει η ανάπτυξη της τεχνολογίας που συμβάλλει στον πλήρη διαχωρισμό κάθε επιστήμης. Ο σημερινός επιστήμονας μελετά και ερμηνεύει μόνο τα δικά του «γνωστικά μονοπάτια »˙  φοράει παρωπίδες και αδιαφορεί για τις αρχές των άλλων επιστημών.

Ας θυμηθούμε τον Πλάτωνα, ο οποίος φρόντισε να περάσει ένα σημαντικό μήνυμα με την εξής επιγραφή στο κτήριο της φημισμένης Ακαδημίας του:

Είναι φανερή η στάση αυτού του καθαρά θεωρητικού επιστήμονα απέναντι στα Μαθηματικά!!!

Στην αρχαιότητα και τη βυζαντινή περίοδο  υπήρχαν  πολλοί γνωστοί φιλόσοφοι-μαθηματικοί. Ο Θαλής, ο Δικαίαρχος, ο Ιππόδαμος, ο Ξενοκράτης, ο Ίππασος, ο Λέων ( βυζαντινή σχολή Μαγναύρας ) κ.α.  Στη σύγχρονη εποχή, ο γνωστός μαθηματικός Μπέρναρντ Μπολζάνο διατύπωσε την εξής φράση: « Ένας αδύνατος μαθηματικός δεν θα γίνει ποτέ δυνατός φιλόσοφος». Η σχέση, λοιπόν, που συνδέει Μαθηματικά και Φιλοσοφία, αλλά και γενικότερα Θεωρητικές και Θετικές επιστήμες είναι τόσο δυνατή που δεν περνά απαρατήρητη από κανέναν.

Ο βασικός συνδετικός κρίκος μεταξύ των δύο επιστημών είναι η έννοια της Λογικής. Όποιος γνωρίζει κάποια Θεωρητική ή Θετική επιστήμη έχει επίγνωση της βασικής τους Λογικής. Είτε Μαθηματικά είτε Αρχαία  ο τρόπος σκέψης είναι περίπου ο ίδιος. Η λογική της απόδειξης, της πλήρους τεκμηρίωσης, της αιτιολόγησης είναι κοινή και για τις δύο επιστήμες.

Οι Θεωρητικές και Θετικές επιστήμες αναπτύσσονται ταυτόχρονα, όσο διαφορετικές και αν είναι. Αλληλοϋποστηρίζονται για να αναπτυχθούν.

Έχοντας κοινή Λογική, εφαρμόζοντας τους ίδιους νοηματικούς κανόνες, οι δύο επιστήμες συμπλέουν αρμονικά. Δεν είναι τυχαίο το γεγονός ότι όποιος είναι καλός στη Σύνταξη των αρχαίων κειμένων είναι και στα Μαθηματικά ή το αντίστροφο. Αφού τα τόσο τα Μαθηματικά όσο και η Σύνταξη είναι Λογική.

Κάθε μαθηματική ανακάλυψη είναι προϊόν φιλοσοφικών αναζητήσεων. Κάθε μαθηματικό μοντέλο χρειάζεται τη συμβολή της Φιλοσοφίας. Κάθε φιλοσοφική ρήση αποτελεί πηγή για τους θετικούς επιστήμονες, δίνοντας ευκαιρίες να ανακαλύψουν  νέες πτυχές του αντικειμένου τους.

Υπάρχει, λοιπόν, τόσο μεγάλο χάσμα ανάμεσα στις Θεωρητικές και τις Θετικές Επιστήμες;

Κατερίνα Β. & Σταμάτης Β.

Πατήστε εδώ για να δείτε την παρουσίαση που ετοιμάσαμε για τους Ιούς των Υπολογιστών.

Η επαυξημένη ή ενισχυμένη πραγματικότητα (AR-Augmented Reality) είναι μια ζωντανή άμεση ή έμμεση άποψη ενός φυσικού πραγματικού περιβάλλοντος, του οποίου τα στοιχεία έχουν αυξηθεί (ή  συμπληρωθεί) από αισθητηριακά ερεθίσματα που έχουν δημιουργηθεί από υπολογιστή, όπως ήχος, βίντεο, γραφικά ή δεδομένα GPS.

Ως αποτέλεσμα, η τεχνολογία λειτουργεί  ενισχύοντας την τρέχουσα αντίληψη κάποιου για την πραγματικότητα.  Αντίθετα, η εικονική πραγματικότητα αντικαθιστά τον πραγματικό κόσμο με μια προσoμοίωσή του .

Τα υλικά εξαρτήματα για την επαυξημένη πραγματικότητα είναι: επεξεργαστής, οθόνη, αισθητήρες και συσκευές εισόδου. Οι σύγχρονες κινητές υπολογιστικές συσκευές όπως τα smartphones και οι υπολογιστές tablet περιέχουν αυτά τα στοιχεία, τα οποία συχνά περιλαμβάνουν μια φωτογραφική μηχανή και αισθητήρες, όπως επιταχυνσιόμετρο, GPS, και πυξίδα, καθιστώντας τες κατάλληλες πλατφόρμες  για AR.

Η εικονική πραγματικότητα παρέχει πληροφορίες με διαδραστικό και ψηφιακό διαχειρισμό τρόπο σχετικά με τον πραγματικό κόσμο που περιβάλλει τον χρήστη . Στις μέρες μας γίνεται εθιστικό . Είναι κερδοφόρα προς εμάς η εικονική πραγματικότητα;

Όλα φυσικά έχουν τα θετικά και τα αρνητικά τους!!!

Κάποια από τα θετικά της είναι ότι με αυτόν τον     τρόπο     μπορούμε να ταξιδεύουμε ψηφιακά σε μέρη τα οποία     απέχουμε χιλιόμετρα μακριά μόνο με ένα «κλικ»      και να περιπλανιόμαστε σε αυτά σαν να είμαστε εκεί ζωντανά! Όπως για παράδειγμα η νέα εφαρμογή της Google Maps όπου μπορούμε να δούμε μέρη  σε 3D μορφή από όλο τον κόσμο .

Ένα δεύτερο παράδειγμα είναι τα videogames όπου με την υψηλή τους ανάλυση και τα φοβερά γραφικά έχουν ως αποτέλεσμα να έχεις την αίσθηση ότι εσύ ο ίδιος είσαι ο ήρωας του παιχνιδιού .

Αντίθετα , όμως , υπάρχει και η αρνητική πλευρά , όταν η χρήση όλων αυτών γίνεται υπερβολική δηλαδή όταν κάποιος εθίζεται . Αυτό έχει ως αποτέλεσμα την σπατάλη    πολύ και χρήσιμου χρόνου και την αντικατάσταση του πραγματικού κόσμου με τον ψηφιακό . Όπως για παράδειγμα πολλά παιδιά στην εφηβεία εθίζονται πολύ εύκολα η για λόγους που νιώθουν μειονεκτικά στο ΄΄ κόσμο ΄΄ τους ή για κάποιο πρόβλημα που έχουν με την εμφάνιση τους ή γιατί τους αρέσουν πολύ τέτοιου είδους απασχολήσεις. Αυτοί οι έφηβοι εθίζονται στους υπολογιστές τους και παραμελούν το σχολείο και πολλές φορές ξεχνούν και τις βασικές τους ανάγκες όπως για παράδειγμα να φάνε , χάνουν την επικοινωνία με τους φίλους και την οικογένεια τους. Και κάτι ακόμα πιο επικίνδυνο και αρκετά συχνό και εύκολο  να πραγματοποιηθεί είναι μέσω αυτών των παιχνιδιών να πέσουν θύματα κακοποίησης.

Για αυτούς τους λόγους και πολλούς ακόμα θα πρέπει να διασκεδάζουμε με αυτά τα παιχνίδια χωρίς να εθιζόμαστε και ΠΑΝΤΑ να έχουμε μετρό!!!

Ο Blaise Pascal ήταν Γάλλος μαθηματικός, φυσικός και θρησκευτικός φιλόσοφος που συνέβαλε στην ανάπτυξη πολλών περιοχών των μαθηματικών.

Δούλεψε στις Κωνικές Τομές στην Προβολική Γεωμετρία και σε συνεργασία με τον Fermat βοήθησε στη θεμελίωση της θεωρίας των πιθανοτήτων. Διατύπωσε αυτό που ονομάζουμε νόμο του Pascal στην πίεση και διέδωσε ένα θρησκευτικό δόγμα που δίδαξε την εμπειρία του Θεού μέσω της καρδιάς παρά μέσω του λόγου.

Το Τρίγωνο του Pascal

Το τρίγωνο του Pascal κατασκευάζεται όπως δείχνει το παρακάτω σχήμα.

Έχει τις εξής ιδιότητες:

• Η 1^η  γραμμή έχει 1 αριθμό, η 2^η γραμμή έχει 2 αριθμούς, η 3^η  γραμμή έχει 3 αριθμούς, κτλ. Η ν-οστή γραμμή έχει ν αριθμούς.
• Οι αριθμοί της ν-οστής γραμμής είναι συντελεστές του αναπτύγματος
• Το άθροισμα των αριθμών κάθε γραμμής είναι ίσο με μια δύναμη του 2
• Οι αριθμοί   1,1, 2, 3, 5, 8, 13, 21… που είναι τα αθροισμάτα των αριθμών  του σχήματος, είναι οι όροι της ακολουθίας που είναι γνωστή με το όνομα «ακολουθία Fibonacci». Ο κάθε όρος της ακολουθίας αυτής από τον τρίτο και μετά είναι ίσος με το άθροισμα των δυο προηγούμενων: 2=1+1, 3=2+1, 5=3+2…

 

 

 

 

 

 

 

 

 

 

 

 

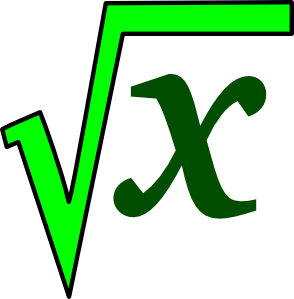Η λέξη ρίζα έχει πολλές σημασίες  σε διαφορετικούς τομείς, για παράδειγμα:

1. Στη βοτανική η λέξη ρίζα είναι το κάτω μέρος του φυτού που βρίσκεται μέσα στο έδαφος.
2. Στη οδοντιατρική ονομάζεται το κάτω μέρος του δοντιού που βρίσκεται μέσα στα ούλα.
3. Στη κομμωτική  ονομάζεται το κάτω μέρος της τρίχας που βρίσκεται μέσα στο δέρμα.
4. Στη χημεία ονομάζεται ομάδα ατόμων που δεν υφίσταται μεταβολή στη διάρκεια μιας χημικής αντίδρασης.
5. Στα μαθηματικά τετραγωνική ρίζα ονομάζουμε έναν (οποιοδήποτε) αριθμό που όταν υψωθεί στο τετράγωνο (δηλαδή πολλαπλασιαστεί με τον εαυτό του) μας δίνει το χ.

Για παράδειγμα η τετραγωνική ρίζα του 25 είναι ο αριθμός 5 επειδή 5Χ5=25 (5²=25 ή √25=5). Το ίδιο ισχύει και με την νιοστή ρίζα, δηλαδή η τετραγωνική ρίζα του χ είναι το α  ( α²=χ ή √_χ=α) . Ο συμβολισμός της τετραγωνικής ρίζας (√) άρχισε να χρησιμοποιείται το 1525 από τον Christoff Rudolf. Η τετραγωνική ρίζα ενός αριθμού α συμβολίζεται με :

• Το ριζικό ή σύμβολο της ρίζας (√) και Την υπόρριζη ποσότητα (α)

 

I. Ρίζες πραγματικών αριθμών

Αν α ≥ 0, η √_α  παριστάνει τη μη αρνητική λύση της εξίσωσης χ²= α . Είναι ο μη αρνητικός αριθμός  χ που όταν υψωθεί  στο τετράγωνο μας δίνει α.

 

II. Ιδιότητες τετραγωνικών ριζών:

√α² =│a│        √a  √β = √αβ         √α/√β = √α/β

 

III. Η Νιοστή ρίζα μη αρνητικού αριθμού:

Η ν-οστή ρίζα ( ν θετικός ακέραιος ) ενός μη αρνητικού αριθμού α συμβολίζεται ^ν√α και είναι ο μη αρνητικός αριθμός που, όταν υψωθεί στη ν δίνει α. Αν α ≥ 0, τότε η ^ω√α παριστάνει τη μη αρνητική  λύση της εξίσωσης χ^ν=α

 

IV. Ιδιότητες ριζών:

Αν α ≥ 0:

• (^ν√α)^ν = α και ^ν√α^ν= α
• ^ν√α  ^ν√β = ^ν√αβ ( Η ιδιότητα αυτή ισχύει και για περισσότερους  από δύο παράγοντες)
• ^ν√α/^ν√β  = ^ν√α/β  (β ≠ 0)
• ^μ√^ν√α = ^μν√α
• ^νρ√α^μρ =  ^ν√α^μ

Αν α,β ≥ Ο και κ θετικός ακέραιος, τότε:

^ν√α^κ = (^ν√α)^κ      και   ^ν√α^ν β = α^ν√β