By Maria Athanasopoulou (A Class)
What is infinity? Is it a number? It is nowhere on the number line. But we often say things like an infinite number of something. As far as we know, infinity could be real. The universe may be infinite in size and flat extending out forever and ever without end, beyond even the part we can observe or ever hope to observe. That’s exactly what infinity is; not a number per se, but a size; the size of something that doesn’t end.
Infinity is not the biggest number; on the contrary, it is the total of numbers that exist. But we have divided infinity in different kinds. The smallest kind is called countable infinity: for instance, the number of hours in forever or the total of whole/natural numbers that exist. Sets like these are unending but they are countable. It means that you can count them from one element to the other in a finite amount of time. Even if that time is longer than you will ever live or the universe will exist, it is still finite. Uncountable infinity on the other hand, is literally bigger; too big to even count. For example, the set of real numbers, not just whole numbers, is called uncountably infinite. You literally cannot count even from zero to one in a finite amount of time by naming every real number in between. Think about it, you start with zero but what comes next? 0,0000000…. eventually we would imagine a 1 going somewhere at the end, but there is no end, we can always add another zero. Uncountability makes this set so much bigger than the set of whole numbers that between one and zero there are more numbers than whole numbers on the entire endless number line.
The mathematical proof of this is called the Diagonal Argument and is fairly simple. First of all, you need to understand that when it comes to infinity two sets are even when there is a one-to-one correspondence. Which brings us to this: imagine listing every number between zero and one. Since they are uncountable and can’t be listed in order, let’s imagine randomly generating them forever with no repeats. Each number we generate can be paired with a whole number. If there is a one-to-one correspondence between the two that would mean that countable and uncountable sets are the same size. But we can’t do that. Even if the list of real numbers goes on forever, forever isn’t enough. If we go diagonally down our endless list of real numbers and take the first dismal of the first number, the second of the second number, the third of the third and so on, and add one to each subtracting one if it happens to be a nine we can generate a new real number, that is obviously between zero and one, but since we have defined it to be different from every number on our endless list, on at least one place it’s clearly not contained in the list. In other words, every single whole number in the entire infinity of them is matched up and we can still come up with more real numbers.
Here is something else that is true but counterintuitive. There is the same number of even numbers as there are even and odd numbers. At first that sounds ridiculous; clearly there are half as many even numbers as there are whole numbers. But that intuition is wrong. The set of whole numbers is denser but every even number can be matched with a whole number. You will never run out of numbers of either set so this one to one correspondence shows that both sets are the same size. So as its turns out infinity divided by two is still infinity ( ∞/2 = ∞). Infinity plus one is also infinity (∞ +1 = ∞). A good illustration of this is Hilbert’s Paradox of the grand hotel.
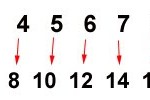
In the 1920’s the German mathematician David Hilbert conducted a famous thought experiment. Imagine a hotel with a countably infinite number of rooms and a very hardworking night manager. One night the infinite hotel is completely full. Totally booked up with an infinite number of guests. A man walks into the hotel and asks for a room. Rather than turning him away the night manager decides to make room for him. He asks the guest in room number 1 to move to room 2, the guest in room number 2 to move to room 3 and so on. Every guest moves from room n to room n+1. Since there are infinite rooms there is a new room for each existing guest. This leaves room 1 open for the new customer. The process can be repeated for any finite number of new guests. If, say, a tour bus unloads 40 new people looking for rooms then every existing guest just moves from room number n to room number n+40; thus opening the first 40 rooms. But now an infinitely large bus with a countably infinite number of passengers pulls up to rent rooms. Countably infinite is the key. The infinite bus of infinite passengers perplexes the manager at first but he realizes there is a way to place each new person. He asks the guest in room 1 to move to room 2, the guest in room 2 to move to room 4, the guest in room 3 to room 6 and so on. Each current guest moves from room number n to room 2n, filling up only the infinite even numbered rooms. By doing this he has now emptied all of the infinitely many odd numbered rooms, which are then taken by the people filing off the infinite bus.
We, humans, are finite creatures. Our lives are small and can only scientifically consider a small part of reality. What’s common for us is only a sliver of what is available; we can only see so much of the electromagnetic spectrum, we can only delve so deep into extensions of space. Common sense applies to that which we can access. But common sense is just that: common. If total sense is what we want, we should be prepared to accept that we shouldn’t call infinity weird or strange. The results we have arrived at by accepting it are valid; true within the system we use to understand, measure, predict and order the universe. Perhaps the system still needs perfecting, but at the end of the day history continues to show us that the universe isn’t strange; we are.
Sources:
http://www.mathpages.com/home/kmath371.htm
https://simple.wikipedia.org/wiki/Hilbert’s_paradox_of_the_Grand_Hotel