Τα μαθηματικά και η μουσική είναι δυο επιστήμες που έχουν πολύ μεγάλη σχέση μεταξύ τους. Στην σύγχρονη αντίληψη η μουσική είναι έκφραση συναισθημάτων ή συνδυασμός ήχων και ηχοχρωμάτων ή μελέτη μουσικών οργάνων. Στην αρχαία Ελλάδα όμως η μουσική είχε βαθύτερη υπόσταση και συνδέονταν άμεσα με τα μαθηματικά και την φιλοσοφία.
Είναι ανούσιο όμως να κάνουμε τον διαχωρισμό ανάμεσα στην «επιστήμη» των μαθηματικών και την «τέχνη» της μουσικής. Στην πραγματικότητα, η επιστήμη των μαθηματικών αποτελεί τέχνη, και η μουσική είναι η επιστήμη της τέχνης. Τα μαθηματικά, με άλλα λόγια, δημιουργούν-κυριεύουν τη μουσική. Αυτή η άποψη διατυπώθηκε για πρώτη φορά πριν από 26 αιώνες στην αρχαία Ελλάδα. Ο Πυθαγόρας (580π.Χ.-496π.Χ) ήταν ο πρώτος που μελέτησε τη μουσική μέσα από τα μαθηματικά.
Πιο συγκεκριμένα ο Πυθαγόρας ήταν αυτός που πρώτος έθεσε τις βάσεις της επιστήμης της Μουσικής με μια επιστημονικά θεμελιωμένη θεωρία της Μουσικής. Ανακάλυψε τη σχέση ανάμεσα στο μήκος των χορδών και το τονικό ύψος που δίνουν.
Η ιστορία του Ιάμβλιχου
Σύμφωνα με την ιστορία του Ιάμβλιχου μια μέρα ο Πυθαγόρας περνούσε έξω από το εργαστήριο ενός σιδερά οπού τέσσερις τεχνίτες χτυπούσαν με τα σφυριά τους ένα μέταλλο,. Παρατήρησε ότι από τα χτυπήματα των διάφορων σφυριών πάνω στο αμόνι εκπέμπονταν ήχοι, που συνέθεταν μια ωραία μουσική. Μπαίνοντας στο εργαστήριο παρατήρησε ότι το μουσικό αποτέλεσμα οφειλόταν στα σφυριά των οποίων τα βάρη ήταν ανάλογα των αριθμών 12, 9, 8, 6 .
Συγκρίνοντας, ως προς το βάρος, το πιο βαρύ σφυρί με τα υπόλοιπα βρήκε ότι:
- Εκείνο που έδινε τον ήχο της «όγδοης αρμονικής» ζύγιζε το μισό του βαρύτερου αφού 6/12=1/2.
- Εκείνο που έδινε τον ήχο της «πέμπτης» ζύγιζε τα δύο τρίτα του βαρύτερου αφού 8/12=2/3.
- Εκείνο που έδινε την «τέταρτη» ζύγιζε τα τρία τέταρτα του βαρύτερου αφού 9/12=2/3.
Οι αναλογίες αυτές δημιουργούν την Αρμονία που για τους Πυθαγόρειους είχε σημασία κυριολεκτικά κοσμική. Οι σχέσεις αυτές περιλάμβαναν τους τέσσερις πρώτους φυσικούς αριθμούς 1, 2, 3, 4, το άθροισμα των οποίων ισούται με το 10, τον ιερό αριθμό των Πυθαγορείων (Τετρακτύς), που τον θεωρούσαν «τέλειο» αριθμό. Περιλάμβαναν ακόμα και τους αριθμούς 6, 8 και 12 που έχουν σχέση με τον «κύβο», αφού αυτός έχει 6 έδρες, 8 κορυφές και 12 ακμές.
Μονόχορδο
Στον Πυθαγόρα αποδίδεται η κατασκευή του «Μονόχορδου». Το μονόχορδο χρησιμοποιήθηκε για τον καθορισμό των μαθηματικών σχέσεων των μουσικών ήχων και ονομάζονταν «Πυθαγόρειος κανών». Βέβαια και άλλοι μεγάλοι μαθηματικοί εργάσθηκαν για τον υπολογισμό των μουσικών διαστημάτων πάνω στον κανόνα, όπως ο Αρχύτας και ο Ερατοσθένης ο Δίδυμος.
Ήταν εντυπωσιακό το γεγονός ότι μόνο οι ακριβείς μαθηματικές σχέσεις έδιναν αρμονικούς ήχους στο μονόχορδο. Όμως, πώς ακριβώς πειραματίστηκαν οι Πυθαγόρειοι σ’ αυτό για την ανάδειξη των σχέσεων μαθηματικών και της μουσικής;
Ο Πυθαγόρας λοιπόν έφτιαξε ένα κουτί σαν ηχείο και το σημάδεψε χωρίζοντάς το σε 12 ίσα τμήματα. Δηλαδή τόσα όσες είναι και οι ακμές του κύβου.
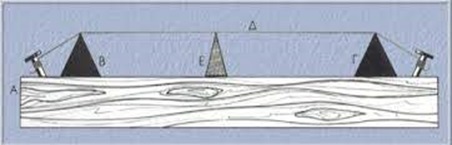Στη συνέχεια κάρφωσε στις άκρες τη χορδή που έχει μέσα το κουτί και χρησιμοποιώντας ένα κινητό καβαλάρη χώρισε την χορδή ερευνώντας το μήκος της και τον μουσικό τόνο που αυτή εκπέμπει.
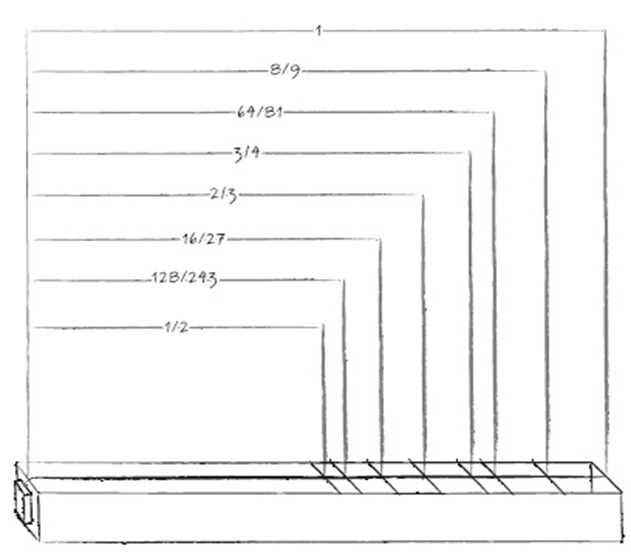
Έτσι ανακάλυψε ότι όταν η χορδή ταλαντώνεται σε όλο το μήκος της βγάζει ήχο που δεν ήταν άλλος παρά ο πρώτος φθόγγος της μουσικής το ντο ή υπάτη όπως την ονόμασαν, με λόγο 1 και συχνότητα 1.
Όταν τοποθέτησε εγκάρσια τον καβαλάρη στη μέση της χορδής τότε δημιουργήθηκε ο όγδοος φθόγγος της μουσικής, το διάστημα της οκτάβας, όπως περιέγραφε ο Πυθαγόρας το ντο ή τη νήτη, κατά τους αρχαίους, με συχνότητα 2/1.
Έτσι ορίστηκαν τα άκρα της μουσικής κλίμακας, η υπάτη και η νήτη.
Μετά μετακινώντας τον καβαλάρη πήγε στον τέταρτο φθόγγο-διαπασών, όπου ταλαντώνονταν τα 3/4 της χορδής, δηλαδή συχνότητα 4/3 και ο τέταρτος φθόγγος από τους οκτώ της μουσικής κλίμακας ήταν γεγονός. Η μέση, δηλαδή το φα.
‘Όταν πήρε τα 2/3 της χορδής δηλαδή συχνότητα 3/2 τότε προέκυψε ο πέμπτος φθόγγος, η παράμεση, το σολ.
Ο δεύτερος φθόγγος προέκυψε από το λόγο του πρώτου, την υπάτη, μετά από πολλαπλασιασμό με 9/8, δηλαδή: 1 x 9/8=9/8, τα 8/9 της χορδής, το ρε.
Ο τρίτος φθόγγος προέκυψε από το λόγο του δεύτερου 9/8, όταν και πάλι πολλαπλασιάστηκε με 9/8 δηλαδή: 9/8 x 9/8=81/64 δηλαδή θα ταλαντώνονται τα 64/81 της χορδής, το μι.
Ο έκτος φθόγγος προέκυψε από το λόγο του πέμπτου την παράμεση, που πολλαπλασιάστηκε με 9/8 δηλαδή: 1:2/3 x 9/8=27/16, γεγονός που σημαίνει πως θα ταλαντώνονταν τα 16/27 της χορδής κι αυτό ήταν το λα.
Τέλος, ο έβδομος φθόγγος προέκυψε από τον λόγο του έκτου, που και πάλι πολλαπλασιάστηκε με 9/8 δηλαδή: 1:16/27 x 9/8=243/128, που σημαίνει ότι για την παραγωγή του θα ταλαντώνονται τα 128/243 της χορδής, άρα θα παράγεται το σι.
Όλα αυτά όμως μπορούμε να τα παρακολουθήσουμε με τη βοήθεια του παρακάτω σχήματος και του πίνακα που ακολουθεί.
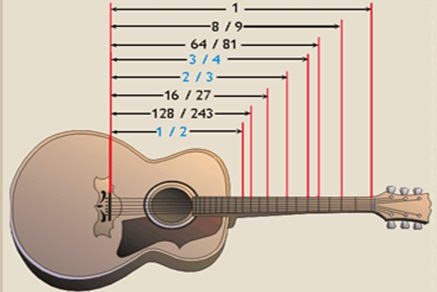Εδώ βλέπουμε τα συμπεράσματα του Πυθαγόρα εφαρμοσμένα στις χορδές μιας κιθάρας .
Μουσική των σφαιρών
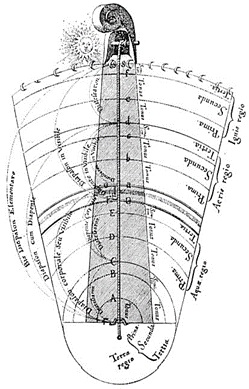Το μονόχορδο του Πυθαγόρα. Με αυτόν τον τρόπο διατύπωσε την σχέση της μουσικής με τα μαθηματικά, αλλά και τις αρμονικές δονήσεις των πλανητών στο ηλιακό μας σύστημα.
Το σημαντικότερο όμως που έκανε ο Πυθαγόρας μέσω αυτής της διαδικασίας ήταν που αντιστοίχισε τους παραγόμενους ήχους στα ουράνια σώματα.
Ο Πυθαγόρας πίστευε, ότι τα ουράνια σώματα είναι διατεταγμένα το ένα σε σχέση με το άλλο με συγκεκριμένες αριθμητικές αναλογίες που εκφράζονται μέσα από ακέραιους και ρητούς αριθμούς, δημιουργώντας την Κοσμική Αρμονία. Αυτή η Τάξη και η Αρμονία που υπάρχει στο Σύμπαν είναι αντίστοιχη με αυτή των μουσικών αναλογιών και προκύπτει από την τέλεια κίνηση των ουράνιων σωμάτων. Η αναλογία αυτή μεταξύ μουσικών διαστημάτων και απόστασης πλανητών εκπροσωπούσε για τον Πυθαγόρα το μυστικό του κόσμου. Γι’ αυτό και ο Πυθαγόρας, καθόρισε τις αποστάσεις των πλανητών με μουσικούς όρους.
Οι Πυθαγόρειοι πίστευαν ότι οι πλανήτες που ήταν σφαίρες, καθώς ταξιδεύουν στον ουρανό παράγουν μουσική λόγω της τριβής τους με τον γαλαξιακό αιθέρα. Πίστευαν ότι η Γη αποτελεί το κέντρο του σύμπαντος και ότι κάθε πλανήτης παράγει τις δικές του νότες, ανάλογα με την απόστασή του από τη Γη. Παράλληλα, διαπίστωναν ότι η μελωδία του σύμπαντος είναι τόσο ξεχωριστή, ώστε τα απλοϊκά αφτιά μας δεν μπορούν να την ακούσουν. Οι πυθαγόρειοι πίστευαν ότι η επίγεια μουσική αποτελεί τη μικρογραφία της μουσικής των σφαιρών. Έτσι θεώρησαν ότι οι νόμοι που διέπουν την επίγεια μουσική ταυτίζονται με αυτούς της ουράνιας αρμονίας. Ωστόσο, πρόκειται για μια μουσική με τόση ισχύ που καθορίζει όλους τους κύκλους της ζωής, από τις τέσσερις εποχές μέχρι τα καιρικά φαινόμενα. Έτσι το μουσικό τους όργανο ήταν συγχρόνως κι ένα τηλεσκόπιο ή ένας αρχέγονος μηχανισμός των Αντικυθήρων. Ήταν ένα όργανο που μελετούσε τα μουσικά διαστήματα αλλά και το διάστημα με τους πλανήτες και τα άστρα.
Σήμερα γνωρίζουμε ότι δεν υπάρχει γαλαξιακός αιθέρας με τον οποίο να έχουν τριβή οι πλανήτες. Όπως γνωρίζουμε ότι δεν υπάρχει πουθενά μέσα στο σύμπαν απόλυτο κενό».
Για τους Πυθαγόρειους, όμως αυτή η άμεση και ακριβής σχέση μαθηματικών, μουσικής και ευχάριστου ψυχικού συναισθήματος αποτελούσε τη μέγιστη απόδειξη ότι η αλήθεια, στο ύψιστο επίπεδό της, εκφράζεται με μαθηματικές σχέσεις. Πίστευαν, μάλιστα, ότι η ψυχή, μέσα από τα μαθηματικά και τη μουσική, μπορούσε να εξυψωθεί ώσπου να ενωθεί με το σύμπαν.
Την ίδια περίπου εμπειρία με τον Πυθαγόρα, της μελέτης των άστρων μέσω της μουσικής, είχε ένας άλλος μεγάλος επιστήμονας ο Γαλιλαίος, ο οποίος μυήθηκε στην πειραματική διαδικασία με τις χορδές από τα λαούτα του πατέρα του Βιντσέντζο Γκαλιλέι, ο οποίος πειραματιζόταν με τρόπο αντίστοιχο με τη μέθοδο του Πυθαγόρα, μελετώντας τις τάσεις των διαφόρων χορδών και των παραγόμενων τονικών υψών.
Στις αρχές της αρμονίας των Πυθαγορείων βασίστηκε η ευρωπαϊκή μουσική μέχρι, τουλάχιστον, τη στιγμή που ο Γιόχαν Σεμπάστιαν Μπαχ, μέσω της σύνθεσής του «Καλοσυγκερασμένο Κλειδοκύμβαλο» πρότεινε την υποδιαίρεση της οκτάβας σε δώδεκα ημιτόνια κάτι που παρεμπιπτόντως είχε προτείνει δύο χιλιάδες χρόνια πριν από τον Μπαχ ο Αριστόξενος, όμως δεν εισακούστηκε. Ο Αριστόξενος, νεότερος του Πυθαγόρα (περί το 375 π.Χ.) υπήρξε φιλόσοφος και σημαντικότατος θεωρητικός της μουσικής και του δόθηκε μάλιστα η ονομασία «ο Μουσικός».
Εκπαιδευτικοί: Τσινόγλου Μαρία, Κατσουρός Δημήτριος
Μαθητές: Καρασούλος Θεόδωρος, Γεώργιος Νικολάου, Ανδρέας Κλάδης,
Δημήτρης Λέπουρας, Λιάκου Παρασκευή
Πηγές:
Από το διαδίκτυο:
- «Μαθηματικά και Μουσική».
- «Μονόχορδο» (Βικιπαίδεια).
- «Τα Μαθηματικά και η Μουσική, δυο επιστήμες που συνδέονται».
- «Το μονόχορδο του Πυθαγόρα και η μουσική κλίμακα».
- «Η μουσική του Πυθαγόρα και η σημασία της στη σημερινή εκπαίδευση».
