ΓΥΜΝΑΣΙΟ (-Α ΤΑΞΗ): ΤΑ ΠΕΝΤΟΜΙΝΟΣ

Τα πεντόμινος είναι ένα σύνολο δώδεκα σχημάτων που έχουν δημιουργηθεί συνδυάζοντας 5 τετράγωνα ή κύβους, με τέτοιο τρόπο ώστε να επιτευχθεί κάθε δυνατός συνδυασμός στην τοποθέτηση τους το ένα δίπλα στο άλλο. Αν παρατηρήσουμε τα πεντόμινος θα προσέξουμε ότι τα σχήματα των πεντόμινος τείνουν να μοιάσουν στα λατινικά γράμματα  F, I, L, N, P, T, U, V, W, X, Y, Z.

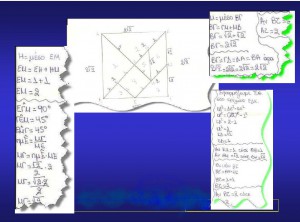
Στο σχήμα κάτω (κέντρο) παρατηρούμε ότι πέντε από τα  πεντόμινος μπορούν να προσανατολιστούν και επομένως να κατασκευαστούν και με εναλλακτικό τρόπο δηλαδή το συμμετρικό του ως προς άξονα συμμετρίας. Μπορούμε να κατασκευάσουμε στο λογισμικό δυναμικής γεωμετρίας Geometer’s Sketchpad (Jackiw, 1991) τα δικά μας πεντόμινος με απλό τρόπο.

Για την κατασκευή τους παρατηρούμε ότι αποτελούνται όλα τα σχήματα πεντόμινος από ίσα τετράγωνα. Όπως καταλαβαίνουμε για να έχουμε την δυνατότητα να συνδυάσουμε τα κομμάτια πεντόμινος πρέπει οι πλευρές των τετραγώνων να είναι ίσες. Η κατασκευή και εφαρμογή των πεντόμινος είναι πολύ σημαντική για την ανάπτυξη οπτικοχωρικών ικανοτήτων στους μαθητές τους μαθητές. Ακόμα για την κατανόηση της συμμετρίας ως προς άξονα.

ΚΑΤΑΣΚΕΥΕΣ ΤΕΤΡΑΠΛΕΥΡΩΝ ΜΕ ΠΕΡΙΣΤΡΟΦΕΣ

Οι κατασκευές πλακοστρώσεων με περιστροφή κατά 180^ο ενός τριγώνου στο Sketchpad είναι  σημαντικές ώστε οι μαθητές να κατανοήσουν την έννοια του συμμετρικού ως προς κέντρο σχήματος. Στα σχήματα κάτω οι μαθητές μπορούν αφού περιστρέψουν το σχήμα του τριγώνου να ερωτηθούν και συμπεράνουν σχετικά με το άθροισμα των γωνιών ενός τριγώνου αλλά και τα είδη των τετράπλευρων που σχηματίζονται όταν το είδος του τριγώνου μεταβάλλεται αφού σύρουμε μια κορυφή του τριγώνου.

Για παράδειγμα στα σχήματα μπορούμε να δούμε ότι το σχήμα του τετράπλευρου μπορεί να είναι παραλληλόγραμμο ή τετράγωνο ή ρόμβος κ.λ.π. Η δραστηριότητα αυτή είναι σημαντική για την διαισθητική κατανόηση της ιεραρχίας των τετράπλευρων, έννοιες που εισάγονται στο τέλος της τάξης της Α Γυμνασίου. Το αιτούμενο είναι η κατανόηση των γεωμετρικών εννοιών μέσα από μια διαδικασία δόμησης των εννοιών και «κατανόηση» για την Κολέζα (2006) σημαίνει «αντίληψη της δομής …(και) πρόβλεψη κατά τη διδασκαλία των κατάλληλων συνδέσεων μεταξύ των εννοιών που μαθεύτηκαν ήδη και εκείνων που οι μαθητές πρόκειται να μάθουν».

ΤΟ ΤΑΝΓΚΡΑΜ (TANGRAM)

Το τανγκράμ (Tangram) είναι ένα κινέζικο παιχνίδι, ένας τύπος puzzle, που αποτελείται από επτά κομμάτια τα λεγόμενα τανς (tans) τα οποία όταν τοποθετηθούν κατάλληλα μπορούν να δημιουργήσουν συγκεκριμένα σχήματα. Ο στόχος είναι να σχηματίσεις το σχήμα με τα επτά κομμάτια, έτσι ώστε το σχήμα να περιέχει όλα τα κομμάτια και κανένα να μην καλύπτει το άλλο.

Στην τάξη της Α Γυμνασίου οι μαθητές μπορούν να χρησιμοποιήσουν έτοιμα κομμάτια τανς προκειμένου να τα συνδυάσουν και να κατασκευάσουν με αυτά άλλα μεγαλύτερα σχήματα. Οι κατασκευές των κομματιών τανς στο λογισμικό και οι υπολογισμοί τους μπορούν να γίνουν στην τάξη της Β Γυμνασίου, ώστε να έχει προηγηθεί εννοιολογικά η εισαγωγή του Πυθαγορείου θεωρήματος ή των τριγωνομετρικών αριθμών του ημιτόνου, συνημίτονου και εφαπτομένης.

ΓΥΜΝΑΣΙΟ–(Β ΤΑΞΗ): ΚΑΠΟΙΑ ΜΑΘΗΜΑΤΙΚΑ ‘ΠΙΣΩ’ ΑΠΟ ΤΙΣ ΚΑΤΑΣΚΕΥΕΣ TESSELLATIONS

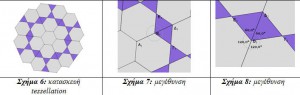
Στην Β τάξη του Γυμνασίου οι μαθητές έχουν την δυνατότητα να εξερευνήσουν μέσω του λογισμικού τις συνθήκες που πρέπει να υπάρχουν για να επιστρώσουμε μια επιφάνεια με ίδια κανονικά πολύγωνα. Θα πρέπει να παρατηρήσουν αρχικά ότι γύρω από ένα σημείο που είναι κορυφή κανονικού πολυγώνου, το οποίο χρησιμοποιούν για την κάλυψη θα πρέπει να υπάρχουν το πολύ 6 και το λιγότερο 3 κανονικά πολύγωνα.

Έξι πολύγωνα γιατί η μικρότερη γωνία ενός κανονικού πολυγώνου είναι 60^ο (ισόπλευρο). Τρία γιατί γύρω από την ίδια κορυφή θα υπάρχουν περισσότερα από δυο κανονικά πολύγωνα αφού κάθε γωνία ενός κανονικού πολυγώνου είναι μικρότερη από 180^ο. Για να γενικεύσουμε τον συλλογισμό μας: γνωρίζουμε ότι αν είναι ν το πλήθος των πλευρών του πολυγώνου τότε η κεντρική γωνία είναι ίση με ω=360^ο/ν και η γωνία φ του πολυγώνου είναι ίση με φ=180^ο-ω =180^ο-(360^ο/ν)=180^ο(ν-2)/ν.

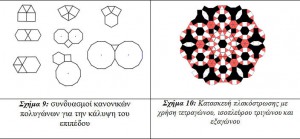
Αν υποθέσουμε ότι ένα κανονικό πολύγωνο με γωνία φ καλύπτει το επίπεδο τότε πρέπει κ*φ= 360^ο, όπου κ είναι ο αριθμός των πολυγώνων με κοινή κορυφή που απαιτούνται να καλύψουν το επίπεδο. Τότε όμως μετά από πράξεις καταλήγουμε ότι 2*(κ+ν)=κ*ν, όπου ν, κ είναι φυσικοί αριθμοί και οι τιμές που μπορεί να πάρει το κ είναι μεγαλύτερες ή ίσες του 3 και μικρότερες ή ίσες του 6. Αν δώσουμε στο κ τιμές και λάβουμε υπόψη τον τύπο επάνω, θα έχουμε την αντιστοιχία: όταν ν=3 τότε κ=6 δηλαδή απαιτούνται 6 ισόπλευρα τρίγωνα (6×60^o =360^o), όταν ν=4 τότε κ=4 δηλαδή απαιτούνται 4 τετράγωνα (4×90^o=360^o)  και όταν ν=6 τότε κ=3 δηλαδή απαιτούνται 3 εξάγωνα , όπως φαίνεται στα σχήματα. Στα σχήματα 6, 7 έχουμε κάνουμε ζουμ στο σημείο επαφής των γωνιών των πολυγώνων. Οι μαθητές μπορούν να παρατηρήσουν ότι οι γωνίες των πολυγώνων σχηματίζουν άθροισμα ίσο με 360^ο. Δηλαδή να οδηγηθούν σε συμπεράσματα σχετικά με το είδος των διαφορετικών κανονικών πολυγώνων που μπορούν να σχηματίσουν μια πλακόστρωση. Πλακοστρώσεις μπορούμε να σχηματίσουμε και με συνδυασμούς κανονικών πολυγώνων, όπως ισοπλεύρων τριγώνων, εξαγώνων, τετραγώνων και δωδεκαγώνων.

Βιβλιογραφία:

Η συγγραφή του κειμένου και η επιλογή των πολυμέσων έγινε από τη Δρ. Σ.Πατσιομίτου. Το κείμενο είναι απόσπασμα της εργασίας

Πατσιομίτου, Σ. (2009) Οι Πλακοστρώσεις στο Sketchpad v4 ως  διαισθητικό θεμέλιο για την ανάπτυξη παραγωγικών συλλογισμών Πρακτικά 1^ου Εκπαιδευτικού Συνεδρίου  ΕΤΠΕ με τίτλο «Ένταξη και χρήση των ΤΠΕ στην Εκπαιδευτική διαδικασία», σσ. 154-160. Βόλος, 24-26 Απριλίου

http://www.etpe.eu/new/custom/pdf/etpe1442.pdf

Πατσιομίτου, Σ. (2009) Επικαλύψεις επιπέδου μέσω του Geometer’s Sketchpad v4 στο Πρόγραμμα Σπουδών: Tessellations, Πεντόμινος, Αλγεβρικές Δομικές μονάδες, Rep-Tiles, Tangram. Πρακτικά 5^ου Πανελλήνιου Συνεδρίου ΤΠΕ, με τίτλο: «Αξιοποίηση των Τεχνολογιών της Πληροφορίας και της Επικοινωνίας στη διδακτική  πράξη», σσ. 601-609. Σύρος 8, 9, 10 Μαΐου 2009

Πατσιομίτου, Σ. (2009) Μαθαίνω Μαθηματικά με το Geometer’s Sketchpad v4 Εκδόσεις Κλειδάριθμος . Τόμος Α . ISBN:978-960-461-308-3

http://eclass.sch.gr/courses/G10114/