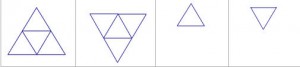
Κανονικότητες στο τρίγωνο του Sierpinski -Οδηγίες κατασκευής σε λογισμικό δυναμικής γεωμετρίας (Πατσιομίτου, Σ)
Πρόκειται για ένα fractal, το οποίο πήρε το όνομά του από τον Πολωνό μαθηματικό Waclaw Sierpinski (1882-1969) το 1915.
Το σχήμα του τριγώνου Sierpinki πρωτο εμφανίστηκε στον Καθεδρικό Ναό του Ravello (τον 12ο αιώνα).[εικόνα κάτω]
Σχήμα 1
Αν Νn είναι ο αριθμός μαύρων τριγώνων μετά από την ν-οστη επανάληψη , Ln το μήκος μιας πλευράς ενός τριγώνου, και An το κλασματικό εμβαδόν που παραμένει μετά από την ν-οστη επανάληψη αφαίρεσης του εσωτερικού τριγώνου, τότε:
(Wolfram 1984; Borwein and Bailey 2003, p. 46)
Για την κατασκευή του τριγώνου του Sierpinski ακολουθούμε τα εξής βήματα.
- Επίπεδο 0: Κατασκευάζουμε ένα ισόπλευρο τρίγωνο
- Ενώνουμε τα μέσα των πλευρών του και αφαιρούμε το εσωτερικό τρίγωνο που σχηματίζεται,έτσι προκύπτει το επόμενο επίπεδο (επίπεδο 1).
- Συνεχίζουμε την ίδια διαδικασία σε κάθε ένα από τα τρία τρίγωνα που σχηματίζονται και οδηγοιύμαστε στο επόμενο επίπεδο (επόπεδο 2).
- Συνεχίζουμε την ίδια διαδικασία σε κάθε τρίγωνο του επιπέδου 2 κ.ο.κ.
Σχήμα 2
Το τρίγωνο Sierpinski με τη βοήθεια λογισμικού δυναμικής γεωμετρίας
Η βασική εργαλειοθήκη των λογισμικών δυναμικής γεωμετρίας περιλαμβάνει εργαλεία για κατασκευή τμημάτων, κύκλων , γραμμών κ.α. Τόσο το Cabri ΙΙ (macros), Geogebra όσο και το Sketchpad (scripts, custom tools) έχουν την προηγμένη δυνατότητα, της προσθήκης στην εργαλειοθήκη νέων εργαλείων και της επαναχρησιμοποίησης τους στις κατασκευές εύκολα και αποτελεσματικά (Straesser ,2003). Για να δημιουργήσουμε ένα νέο εργαλείο, δημιουργούμε αρχικά την γενική κατασκευή που θέλουμε να καθορίσουμε ως εργαλείο. Αυτή η κατασκευή θα χρησιμεύσει και ως o «ορισμός» για τη δημιουργία του εργαλείου. Στο Sketchpad (version 4) για να δημιουργήσουμε την κατασκευή χρησιμοποιούμε οποιαδήποτε διαθέσιμα εργαλεία και εντολές από το menu-Construct, Transform , Measure, and Graph. Έτσι μας επιτρέπεται να εμπλουτίσουμε το μαθηματικό λεξιλόγιο του λογισμικού με τόσες νέες διαδικασίες όσες και επιθυμούμε. Το custom tool μπορεί να περιλαμβάνει ακόμα και action buttons που απαιτούνται για την κατασκευή, ενώ δημιουργούν μαθηματικά αντικείμενα -αποτελέσματα άλλων δεδεομένων αντικειμένων. Αν για παράδειγμα κατασκευάσουμε την μεσοκάθετο ευθ. τμήματος και την αποθηκεύσουμε ως εργαλείο custom tool έχουμε στη συνέχεια τη δυνατότητα κατασκευής του περικέντρου με τρεις επαναλήψεις του εργαλείου . H αποθήκευση στην εργαλειοθήκη μπορεί να γίνει μέσα από το Create New Tool. To νέο εργαλείο που κατασκευάζουμε λειτουργεί πλέον αυτόματα όταν το επιλέξουμε από την εργαλειοθήκη, χωρίς να χρειάζεται να εμφανίσει τα ενδιάμεσα σημεία κατασκευής. Αυτό όχι μόνο μπορεί να οδηγήσει σε συνθετότερες κατασκευές αλλά οδηγεί σε υψηλότερα επίπεδα αφαίρεσης (Πατσιομίτου,2005, 2006).
Για την κατασκευή του τριγώνου Sierpinski
Ανοίγουμε ένα νέο αρχείο στο Sketchpad v4. Η κατασκευή θα γίνει αρχικά σε ισόπλευρο τρίγωνο ώστε οι μαθητές να διαπιστώσουν κάποιες κανονικότητες στο σχήμα ενώ προτείνεται να ακολουθήσουν τα παρακάτω βήματα.
1ο βήμα :
Πως κατασκευάζουμε ένα ισόπλευρο τρίγωνο: επιλέγουμε το ευθύγραμμο τμήμα από την εργαλειοθήκη του λογισμικού και κατασκευάζουμε με αυτό ευθ. τμήμα ΒΓ
- Επιλέγουμε το Β και το τμήμα ΒΓ ταυτόχρονα και από το μενού construct –circle by center and radius (κατασκευή κύκλου από κέντρο και ακτίνα). Ομοίως για το σημείο Γ . Για να βρούμε τα σημεία τομής επιλέγουμε τους κύκλους και από το μενού construct –intersection (κατασκευή σημείου τομής). Αν Α το σημείο τομής των δυο κύκλων το τρίγωνο ΑΒΓ είναι ισόπλευρο
- Επιλέγουμε τους κύκλους και το δεύτερο σημείο τομής. Από το μενού display- hide objects (κρύψε τα αντικείμενα).
2ο βήμα :Πως μπορούμε να φτιάξουμε ένα αρχείο εντολών που θα κατασκευάζει ένα ισόπλευρο επαναλαμβανόμενες φορές; Επιλέγουμε το ισόπλευρο τρίγωνο που μόλις κατασκευάσαμε και από το μενού edit –select all (επιλογή όλων). Στην συνέχεια create new tool (δημιουργία νέου εργαλείου) και στο εικονίδιο που εμφανίζεται γράφουμε το όνομα του αρχείου «ΙΣΟΠΛΕΥΡΟ ΤΡΙΓΩΝΟ». Αν δοκιμάσουμε το εργαλείο μας σε δυο διαφορετικά σημεία στην οθόνη διαπιστώνουμε ότι επαναλαμβάνεται το ισόπλευρο τρίγωνο πάντα εξαρτώμενο από το μήκος του αρχικού τμήματος κατασκευής. Για να δούμε τα βήματα του εργαλείου επιλέγουμε show script view και από το εικονίδιο βλέπουμε τα διαδοχικά βήματα του τρόπου με τον οποίο κατασκευάσαμε το ισόπλευρο.
Στη συνέχεια προτείνονται κάποια διερευνητικά βήματα κατασκευής :
Συνδέστε τα μέσα της κάθε πλευράς από το μενού Construct –midpoint. Πόσα ισόπλευρα τρίγωνα τώρα έχετε; Μπορείτε να επιβεβαιώσετε το συμπέρασμα σας χρησιμοποιώντας το αρχείο εντολών του ισοπλεύρου που μόλις κατασκευάσατε ;
Σχήμα 3
3ο βήμα : Κατασκευάστε τρίγωνο και αλλάξτε την θέση της κορυφής . Πόσα τρίγωνα με την κορυφή προς τα πάνω και πόσα τρίγωνα με την κορυφή προς τα κάτω περιέχονται στα αρχικά τρίγωνα. Γράψτε τις παρατηρήσεις σας.
4ο βήμα : Κατασκευάστε ένα εργαλείο που να επαναλαμβάνει την προηγούμενη κατασκευή (με τους υπολογισμούς εμβαδών) και στην συνέχεια επαναλάβετε την στα μέσα του αρχικού τριγώνου .
Σχήμα 5
5ο βήμα:
Στον παρακάτω πίνακα να τοποθετήσετε τον αριθμό των μπλέ τριγώνων που σχηματίζονται σε κάθε βήμα
|
Βήμα |
Αριθμός μπλέ τριγώνων |
|
1 |
3 |
|
2 |
9 |
Πως αυξάνεται ο αριθμός των μπλέ τριγώνων κάθε βήματος ;
Ανακαλύψτε έναν κανόνα (pattern) ώστε να προβλέψετε τον αριθμό των μπλέ τριγώνων του 4ου , 5ου και νου βήματος ………………………………………………………………………………………………
6ο βήμα
Στον παρακάτω πίνακα να τοποθετήσετε το εμβαδόν των μπλέ τριγώνων που σχηματίζονται σε κάθε βήμα
|
Βήμα |
Εμβαδόν μπλέ τριγώνων |
|
1 |
3/4 |
|
2 |
9/16 |
Τι σχέση υπάρχει ανάμεσα στα εμβαδά των μπλέ τρίγωνων κάθε βήματος ;
Πως προκύπτει ο αριθμός του εμβαδού του 2ου βήματος ;
Μπορείτε να ανακαλύψετε έναν κανόνα (pattern) ώστε να προβλέψετε το εμβαδόν των μπλέ τριγώνων του 4ου , 5ου και νου βήματος ;
………………………………………………………………………………………………
Στον παρακάτω πίνακα να τοποθετήσετε την περίμετρο των μπλέ τριγώνων που σχηματίζονται σε κάθε βήμα
|
Βήμα |
Περίμετρος μπλέ τριγώνων |
|
1 |
3/2 |
|
2 |
9/4 |
Τι σχέση υπάρχει ανάμεσα στις περιμέτρους των μπλέ τριγώνων κάθε βήματος ;
Πως προκύπτει ο αριθμός της περιμέτρου του 2ου βήματος ;
Μπορείτε να ανακαλύψετε έναν κανόνα (pattern) ώστε να προβλέψετε την περίμετρο των μπλέ τριγώνων του 4ου , 5ου και νου βήματος
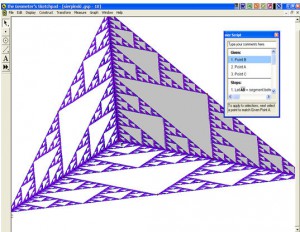
Κατασκευή και εφαρμογή του Sierpinski σε πυραμίδα
Κατασκευάζουμε αρχικά ένα τυχαίο τρίγωνο και στην συνέχεια τα μέσα των πλευρών του Ονομάζουμε τα σημεία των κορυφών του τριγώνου και τα μέσα των πλευρών του. Στην συνέχεια επιλέγουμε τα σημεία Α,Β,C και από το μενού transform-iterate αντιστοιχούμε τις κορυφές του αρχικού τριγώνου με τις κορυφές του τρίγωνου DBF. Από το Structure κατασκευάζουμε και ένα δεύτερο mapping των ίδιων σημείων. Στο σχήμα 10 βλέπουμε μια προ-εικόνα του τριγώνου του Sierpinski όπως έχει ήδη εμφανιστεί στην οθόνη μας .Αν επιλέξουμε το σχήμα και (+) το σχήμα αυξάνει τις υποδιαιρέσεις , ενώ αν επιλέξουμε το( –) τις μειώνει .
Εφαρμογή της κατασκευής: Κατασκευάζουμε μια πυραμίδα και εφαρμόζουμε στις πλευρές της το custom tool που κατασκευάσαμε με τον τρόπο που μόλις αναφέραμε. Οι μαθητές με την περιστροφή του σχήματος ή την αλλαγή προσανατολισμού του ή την αυξομείωση επιπέδων λόγω της διαδικασίας iteration μπορούν να οδηγηθούν σε παρατηρήσεις στο τρισδιάστατο σχήμα[π.χ σχετικά με τα μέσα των πλευρών των τριγώνων στις έδρες του σχήματος ]
Βιβλιογραφία
To άρθρο περιέχει αποσπάσματα των εργασιών στη συνέχεια. Η συγγραφή του άρθρου και η επιλογή των πολυμέσων έγινε από τη Δρ. Σταυρούλα Πατσιομίτου
Σταυρούλα Πατσιομίτου (2005) Τα fractals ως πλαίσιο κατανόησης ακολουθίας και ορίων μέσω της έννοιας τω εμβαδών σε περιβάλλον βασισμένο στο δυναμικό χειρισμό μαθηματικών αντικειμένων. Διπλωματική εργασία Διαπανεπιστημιακού Μεταπτυχιακού Προγράμματος Πανεπιστημίου Αθηνών και Πανεπιστημίου Κύπρου.
Πατσιομίτου, Σ. (2007) Το τρίγωνο του Sierpinski, H σπείρα Baravelle και το Πυθαγόρειο δέντρο. Το Geometer’s Sketchpad v4 στην διαδικασία κατασκευής Fractals με στόχο την κατασκευή εννοιών. Πρακτικά 4ου Πανελλήνιου Συνεδρίου ΤΠΕ με τίτλο: «Αξιοποίηση των Τεχνολογιών της Πληροφορίας και της Επικοινωνίας στη διδακτική πράξη», σσ.28-37, Σύρος, 4-6 Μαΐου 2007
https://www.academia.edu/3540358/_Sierpinski_H_Baravelle_._Geometers_Sketchpad_v4_Fractals_
http://christianhubert.com/writings/fractals.html
Σχολιάστε
Για να σχολιάσετε πρέπει να συνδεθείτε.