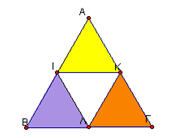
Κατασκευή σπείρας Baravelle σε ισόπλευρο τρίγωνο

• Κατασκευάζουμε ένα ισόπλευρο τρίγωνο  [με τη βοήθεια ενός κατάλληλου αρχείου εντολών ή όχι]

Επιλέγουμε τις πλευρές και από το μενού  construct – midpoint (κατασκευή μέσου) κατασκευάζουμε τα μέσα των πλευρών. 

Επιλέγουμε τα Α,Ι,Κ και από το μενού construct–interior κατασκευάζουμε το εσωτερικό του  τριγώνου.

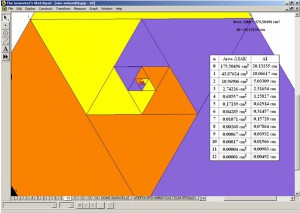
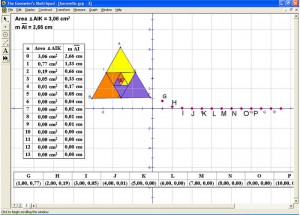
• Επιλέγουμε το τρίγωνο ΑΙΚ και από το μενού Μeasure >>Αrea (perimeter) μετράμε το εμβαδόν (ή την περίμετρο). Επαναλαμβάνουμε την διαδικασία για τα τρίγωνα ΒΙΛ , KΛΓ (ενώ αλλάζουμε τα χρώματα όπως στο σχήμα). Επιλέγουμε τα Α, Β και από το μενού  transform –iterate (μετασχηματίζω-επαναλαμβάνω) αντιστοιχούμε τα σημεία Β,Γ στα Ι,Λ αντίστοιχα. Οι αρχικές μετρήσεις οδηγούν στην εμφάνιση ενός πίνακα του οποίου τα δεδομένα είναι οι μετρήσεις  των εμβαδών και των πλευρών  στις διαδοχικές επαναλήψεις των τριγώνων  του σχήματος.  Η αντιγραφή και επικόλληση του πίνακα του Sketchpad σε φύλλο στο  Excel μας δίνει μεγαλύτερη ευχέρεια στους υπολογισμούς .

• Αν  επιλέξουμε τον πίνακα και με δεξί κλικ επιλέξουμε plot table data (αποτύπωση δεδομένων πίνακα ) παίρνουμε  μια γραφική παράσταση της ακολουθίας  ενώ από το menu-measure-coordinates με επιλογή των σημείων έχουμε τις ακριβείς θέσεις των σημείων. Αυτό έχει σαν συνέπεια ο μαθητής να μπορεί να διαπιστώσει άμεσα τις θέσεις των σημείων του πίνακα στην γραφική παράσταση και επομένως το περιβάλλον του λογισμικού να λειτουργεί ως περιβάλλον πολλαπλών αναπαραστάσεων, οι οποίες   λειτουργούν συμπληρωματικά ενώ  έχουν την δυνατότητα να διευκολύνουν την μάθηση των εννοιών του ορίου και της ακολουθίας (Πατσιομίτου ,2005)

• Αν κάνουμε  zoom με το dilate tool  στο κέντρο του σχήματος οι μαθητές μπορούν να διαπιστώσουν (εξαρτώμενο από το πλήθος των iterations που έχουμε κάνει) ότι η κατασκευή επαναλαμβάνεται και το σχήμα ως fractal τους οδηγεί να κατανοήσουν  μια χαρακτηριστική ιδιότητα των fractal αντικειμένων την  αυτοομοιότητα .
• Αν αλλάξουμε τον τρόπο κατασκευής της σπείρας  δηλαδή κατασκευάσουμε  ισόπλευρο τρίγωνο ABΓ  και από τις κορυφές του φέρουμε παράλληλες προς τι απέναντι πλευρές του τότε το σχήμα  ΔΕΖ  που προκύπτει  είναι πάλι ένα ισόπλευρο τρίγωνο. Η  εφαρμογή της διαδικασίας transform-iteration  με pre-image τις κορυφές του αρχικού ισοπλεύρου και first-image τις κορυφές του ισοπλεύρου που μόλις κατασκευάσαμε δίνει σαν αποτέλεσμα την κατασκευή μιας αύξουσας ακολουθίας εμβαδών (ή περιμέτρων). Ακόμα οι παρατηρήσεις των μαθητών μέσα από το zoom αλλά και τις μετρήσεις ,  μπορούν να τους οδηγήσουν στην απόκτηση μιας ισχυρής διαίσθησης σχετικά με  το άπειρο και τα απειροελάχιστα (Πατσιομίτου ,2005) . 

Σημείωση: Το αρθρο είναι απόσπασμα των παρακάτω εργασιών που αναφέρονται στις βιβλ. αναφορές. Η επιμέλεια του άρθρου και η επιλογή των πολυμέσων έγινε από τη Δρ. Σ.Πατσιομίτου

Βιβλιογραφικές αναφορές

Σταυρούλα Πατσιομίτου (2005) Τα fractals ως πλαίσιο κατανόησης  ακολουθίας και ορίων μέσω της έννοιας τω εμβαδών σε περιβάλλον βασισμένο στο δυναμικό χειρισμό μαθηματικών αντικειμένων. Διπλωματική εργασία Διαπανεπιστημιακού Μεταπτυχιακού Προγράμματος Πανεπιστημίου Αθηνών και Πανεπιστημίου Κύπρου.

http://www.math.uoa.gr/me

Πατσιομίτου, Σ. (2009) Μαθαίνω Μαθηματικά με το Geometer’s Sketchpad v4 Εκδόσεις Κλειδάριθμος . Τόμος Β. ISBN:978-960-461-309-0

Πατσιομίτου, Σ. (2007)  Το τρίγωνο του Sierpinski, H σπείρα  Baravelle και το Πυθαγόρειο δέντρο. Το Geometer’s Sketchpad v4 στην διαδικασία κατασκευής Fractals με στόχο την κατασκευή εννοιών. Πρακτικά 4ου Πανελλήνιου Συνεδρίου ΤΠΕ με τίτλο: «Αξιοποίηση των Τεχνολογιών της Πληροφορίας και της Επικοινωνίας στη διδακτική  πράξη», σσ.28-37, Σύρος, 4-6 Μαΐου 2007

https://www.academia.edu/3540358/_Sierpinski_H_Baravelle_._Geometers_Sketchpad_v4_Fractals_