Η Αλγεβρα Boole (Boolean algebra) πήρε το όνομά της από τον G. Boole (1815-1864), ο οποίος ανέπτυξε ένα αλγεβρικό σύστημα (1854) για τη συστηματική αντιμετώπιση της λογικής. Τα αξιώματα της Αλγεβρας Boole διατυπώθηκαν από τον E. V. Huntington (1904).
Οι μεταβλητές που χρησιμοποιούνται στην Αλγεβρα Boole ονομάζονται λογικές μεταβλητές γιατί μπορούν να πάρουν δύο (2) μόνο τιμές: 0 και 1. Αυτός είναι ο λόγος που η Αλγεβρα Boole αποτελεί τη βάση για τα ψηφιακά ηλεκτρονικά κυκλώματα.
Στην Αλγεβρα Boole ορίζονται τρεις βασικές πράξεις:
α) η πράξη NOT (ΟΧΙ) με σύμβολο – (π.χ. Ã ) και διαβάζεται συμπλήρωμα Α
β) η πράξη AND (ΚΑΙ) με σύμβολο ·
γ) η πράξη OR (Η) με σύμβολο +
Ωστόσο το 1938 ο C. Shannon έδειξε ότι η Άλγεβρα Boole μπορούσε να εφαρμοστεί στην απλοποίηση και στη σχεδίαση των ηλεκτρονικών κυκλωμάτων, όπως, για παράδειγμα στα τηλεφωνικά κυκλώματα. Αργότερα χρησιμοποιήθηκε για τη σχεδίαση των κυκλωμάτων των υπολογιστών.
Τα ηλεκτρονικά κυκλώματα που εκτελούν τις βασικές πράξεις της Άλγεβρας Boole καλούνται λογικές πύλες. Κάθε τέτοια πύλη δέχεται στην είσοδό της σήματα με τη μορφή υψηλής ή χαμηλής ηλεκτρικής τάσης και δίνει στην έξοδό της ένα μοναδικό λογικό αποτέλεσμα με τη μορφή υψηλής ή χαμηλής ηλεκτρικής τάσης. Συνδυάζοντας κατάλληλα λογικές πύλες δημιουργούνται πιο σύνθετα κυκλώματα που μπορούν να εκτελούν λογικές πράξεις.
Αρχικά για την υλοποίηση των λογικών πυλών χρησιμοποιήθηκαν διακριτά ηλεκτρονικά στοιχεία. Σήμερα στα ολοκληρωμένα κυκλώματα υπάρχει ένα μεγάλο πλήθος επιμέρους κυκλωμάτων, τα οποία με τη σειρά τους αποτελούνται από πλήθος λογικών πυλών.
Οι λογικές πύλες είναι τα βασικά δομικά στοιχεία στα ψηφιακά κυκλώματα. Όπως έχουμε στις οικοδομές τα τούβλα και με αυτά κατασκευάζουμε τοίχους και σύνθετες κατασκευές χρησιμοποιώντας παρόμοια υλικά ξανά και ξανά, έτσι και στα ψηφιακά κυκλώματα χρησιμοποιούμε τις λογικές πύλες για να κατασκευάσουμε σύνθετα κυκλώματα.
ΒΑΣΙΚΕΣ ΛΟΓΙΚΕΣ ΠΥΛΕΣ
Βασικές λογικές πύλες είναι οι:
- ΟΧΙ (NOT)
- ΚΑΙ (AND)
- Ή (OR)
- Αποκλειστικό Ή (XOR)
- ΟΧΙ-ΚΑΙ (NAND)
- ΟΧΙ – Ή (NOR)
Πύλη NOT
Η πύλη NOT (ΟΧΙ) έχει μόνο μία είσοδο και δίνει μόνο μία έξοδο. Η λειτουργία της είναι η αντιστροφή του λογικού σήματος της εισόδου.
Ο πίνακας αληθείας της πύλης είναι:
|
Είσοδος |
Έξοδος |
|
A |
ΟΧΙ A |
|
0 |
1 |
|
1 |
0 |
Το κυκλωματικό σχεδιάγραμμα είναι το εξής:
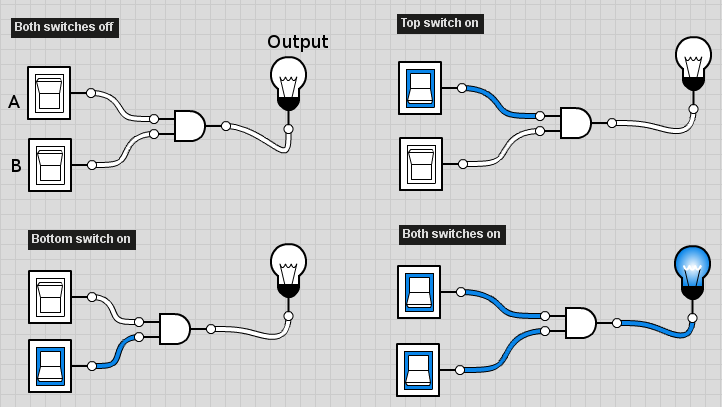
Πύλη AND
Η πύλη AND εκτελεί την λογική πράξη AND (ΚΑΙ) μεταξύ των εισόδων της. Η πράξη AND στην άλγεβρα Boole συμβολίζεται με επί (*). Για παράδειγμα εαν η πύλη έχει 2 εισόδους (a και b) και μία έξοδο (c) θα γίνει η πράξη:
Ο πίνακας αληθείας της λογικής πύλης AND φαίνεται στο εξής σχήμα:
| Είσοδοι | Έξοδος | |
|
A |
B |
A ΚΑΙ B |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Το κυκλωματικό σχήμα της AND 2 εισόδων είναι το εξής:
Παράδειγμα: έστω ότι a=1 και b=0. Η έξοδος c θα προκύψει 0.
Γενικότερα, η έξοδος AND δίνει λογική έξοδο 1 όταν όλες οι είσοδοί της βρίσκονται σε λογική κατάσταση 1.
Οι πύλες AND κατασκευάζονται και με περισσότερες των δύο εισόδων (πχ 3,4,5,8 είσοδοι).
Πύλη OR
Η πύλη OR εκτελεί την λογική πράξη OR (Η΄) μεταξύ των εισόδων της. Η πράξη OR στην άλγεβρα Boole συμβολίζεται με το συν (+). Για παράδειγμα εαν η πύλη έχει 2 εισόδους (a και b) και μία έξοδο (c) θα γίνει η πράξη:
Ο πίνακας αληθείας της λογικής πύλης OR φαίνεται στο εξής σχήμα:
|
Είσοδοι |
Έξοδος |
|
|
A |
B |
A Η” B |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
Το κυκλωματικό σχήμα της OR 2 εισόδων είναι το εξής:
Παράδειγμα: Έστω ότι a=1 και b=0. Η έξοδος c θα προκύψει 1.
Γενικότερα, η πύλη OR δίνει λογικό 1 όταν μία τουλάχιστο είσοδος είναι σε λογικό 1.
Οι πύλες OR κατασκευάζονται και με περισσότερες των δύο εισόδων (πχ 3,4,5,8 είσοδοι).
Πύλη XOR
Η πύλη XOR εκτελεί την λογική πράξη XOR (ΑΠΟΚΛΕΙΣΤΙΚΟ Η’) μεταξύ των εισόδων της. Η πράξη XOR στην άλγεβρα Boole συμβολίζεται με ένα συν μέσα σε ένα κύκλο (⊕).Για παράδειγμα εαν η πύλη έχει 2 εισόδους (a και b) και μία έξοδο (c) θα γίνει η πράξη:
Ο πίνακας αληθείας της λογικής πύλης ΧOR φαίνεται στο εξής σχήμα:
|
Είσοδοι |
Έξοδος |
|
|
A |
B |
A XOR B |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
Το κυκλωματικό σχήμα της XOR 2 εισόδων είναι το εξής:
Παράδειγμα: Έστω ότι a=1 και b=0. Η έξοδος c θα προκύψει 1.
Γενικά η πύλη XOR ελέγχει την περιττή ισοτιμία, δηλαδή δίνει λογικό 1 όταν περριτός αριθμός εισόδων βρίσκεται σε λογικό 1.
Πύλη NAND
Η πύλη NAND (ΟΧΙ-ΚΑΙ) δίνει την αντίθετη έξοδο από την AND, δηλαδή δίνει λογικό 1 όταν υπάρχει τουλάχιστο ένα λογικό 0 στις εισόδους.
Ο πίνακας καταστάσεων και το κυκλωματικό σχεδιάγραμμα είναι τα εξής:
|
Είσοδοι |
Έξοδος |
|
|
A |
B |
A NAND B |
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
Πύλη NOR
Η πύλη NΟR (ΟΧΙ-Η’) δίνει την αντίθετη έξοδο από την OR, δηλαδή δίνει λογικό 1 όταν και οι δύο είσοδοι είναι 0. Ο πίνακας καταστάσεων και το κυκλωματικό σχεδιάγραμμα είναι τα εξής:
|
Είσοδοι |
Έξοδος |
|
|
A |
B |
A NOR B |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
0 |
Πύλη ΧNOR
Η πύλη ΧNΟR δίνει την αντίθετη έξοδο από την ΧOR, δηλαδή δίνει λογικό 1 όταν οι δύο είσοδοι είναι στην ίδια λογική στάθμη. Ο πίνακας καταστάσεων και το κυκλωματικό σχεδιάγραμμα είναι τα εξής:
|
Είσοδοι |
Έξοδος |
|
|
A |
B |
A XNOR B |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
ΠΙΝΑΚΑΣ :
Δοκιμάστε και μόνοι σας
Μπορείτε να δοκιμάστε και μόνοι σας τις λογικές πύλες στους παρακάτω συνδέσμους:
http://www.neuroproductions.be/logic-lab/
ΒΙΝΤΕΟ :
ΠΗΓΕΣ :
- http://ebooks.edu.gr/modules/ebook/show.php/DSGL-C127/577/3739,16398/
- https://el.wikipedia.org/wiki/%CE%9B%CE%BF%CE%B3%CE%B9%CE%BA%CE%AE_%CF%80%CF%8D%CE%BB%CE%B7
- http://users.sch.gr/kgiannaras/mathimata/psifiaka-ilektronika/logikes-pyles-kai-pinakes-alitheias.html
Το κυκλωματικό σχεδιάγραμμα είναι το εξής: