Όλοι γνωρίζουμε τον αριθμό π, όμως ποιός γνωρίζει τον αριθμό φ; Είναι όπως και ο π άρρητος και προκύπτει απο την διαίρεση δύο αριθμών, όταν ισχύει (για α > b):
Τα πρώτα δέκα ψηφία του έχουν ως εξής: 1,618033988…
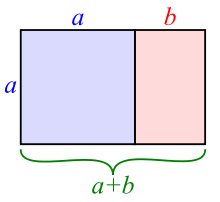
Θα μπορούσαμε να πούμε ότι είναι ο λόγος μεταξύ δύο τμημάτων ή ποσοτήτων τα οποία έχουν αναλογία χρυσής τομής. Αναφέρεται επίσης ως χρυσός λόγος ή χρυσός κανόνας ή χρυσή μετριότητα ή Θεϊκή αναλογία ή άκρος και μέσος όρος. Χρυσό λέγεται κάθε ισοσκελές τρίγωνο στο οποίο ο λόγος της μεγάλης πλευράς προς τη μικρή θα είναι ίσος με φ.Κάθε ισοσκελές με γωνία κορυφής 36μοίρες είναι χρυσό. Επίσης, φέρνοντας τη διχοτόμο μιας από τις παρά τη βάση γωνίες, αυτή δημιουργεί στην απέναντι πλευρά χρυσή τομή. Χρυσό ορθογώνιο λέγεται κάθε ορθογώνιο το οποίο έχει λόγο πλευρών ίσο με φ.
Όι ιδιότητες της χρυσής τομής συνεπαίρνουν την ανθρωπότητα εδώ και 2.400 χρόνια. Πρώτοι οι Αρχαίοι Έλληνες μελέτησαν σημασία της στην γεωμετρία των πενταγράμμων και ιδιαίτερα ο Πυθαγόρας. Ο προηγούμενος είχε μάλιστα πεί ότι ο λόγος του εμβαδού ενός κανονικού πενταγώνου προς το εμβαδόν του πενταγώνου που σχηματίζεται απο το αστέρι που έχει τις γωνίες του στις γωνίες του αρχικού πενταγώνου ειναι ίσος με τον φ. Αργότερα ο Ευκλείδης έδωσε τον πρώτο ορισμό για την χρυσή τομη: «Μια ευθεία γραμμή λέγεται ότι έχει κοπεί σε άκρο και μέσο λόγο, όταν όλη η ευθεία είναι για το μεγαλύτερο κομμάτι ότι είναι το μεγαλύτερο κομμάτι για το μικρότερο». O αριθμός Φ έχει πάρει το όνομα του – Συμβολισμό από τον Φειδία , ο οποίος ήταν ο πρώτος που τον χρησιμοποίησε .
Ο Φειδίας ήταν Αθηναίος Γλύπτης (5ος αιώνας π.Χ) και στενός συνεργάτης του Περικλή. Τρία αγάλματα της Αθηνάς έστεισε ο Φειδίας στην Ακρόπολη: την Πρόμαχο, τη Λημνία και τη Χρυσελεφάντινη. Από το 490 π.Χ. μέχρι και το 1931 μ.Χ. πολλοί ασχολήθηκαν με τον αριθμό φ. Μεταξύ αυτών είναι ο Πλάτων, ο Φιμπονάτσι, ο Γιοχάνες Κέπλερ, ο Μάρτιν Όμ κ.α. Η αναλογία χρησιμοποιήθηκε και ακόμη χρησιμοποιείται απο καλλιτέχνες και αρχιτέκτονες γιατί πιστεύουν ότι είναι αισθητικά ευχάριστη. Κάποιοι υποστήριξαν ότι στοιχεία της πρόσοψης του Παρθενώνα εμφανίζουν χρυσές αναλογίες πράγμα που άλλοι διαψεύδουν. Τέσσερα σπάνια παραδείγματα εφαρμογής αναλογιών χρυσής τομής εντοπίσθηκαν σε ένα αρχαίο πύργο της Μεθώνης Μεσσηνίας, στο Μεγάλο Βωμό της Περγάμου, σε μια επιτύμβια στήλη από την Έδεσσα και σε ένα μνημειακό τάφο στην Πέλλα.
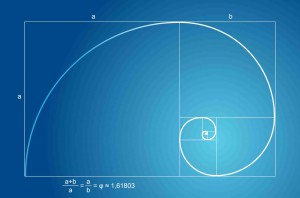
Ως και στην μουσική χρησιμοποιήθηκε η χρυσή αναλογία. Από κάποιες εταιρίες εφαρμόζεται στα μουσικά όργανα και ο γάλλος συνθέτης Ερίκ Σατιέ χρησιμοποίησε τη χρυσή αναλογία σε πολλά από τα κομμάτια του. H σημασία της Χρυσής Τομής όμως δεν περιορίζεται στις καλές τέχνες. Ενδιαφέρουσες εφαρμογές ξεκινούν από την κατασκευή, με τη βοήθεια της Χρυσής Τομής, ενός άλλου γεωμετρικού σχήματος, που ονομάζεται Λογαριθμική Σπείρα.
H κατασκευή αυτή βασίζεται στην ακόλουθη ιδιότητα των «χρυσών» ορθογωνίων. Αν «κόψουμε» ένα τετράγωνο από ένα τέτοιο ορθογώνιο, τότε το μικρότερο ορθογώνιο που απομένει είναι πάλι «χρυσό»! Με τον τρόπο αυτόν μπορούμε να κατασκευάσουμε μια ακολουθία από ολοένα και μικρότερα «χρυσά» ορθογώνια, που βρίσκονται το ένα μέσα στο άλλο. H λογαριθμική σπείρα είναι το σχήμα που σχηματίζεται σε αυτή την ακολουθία των χρυσών ορθογωνίων, αν εγγράψουμε σε κάθε τετράγωνο ένα τεταρτοκύκλιο. Όμως, οι άνθρωποι δεν είναι οι μόνοι που χρησιμοποιούν χρυσές αναλογίες.
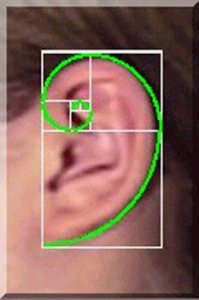
Και στην φύση εμφανίζονται πολλές. Ερευνητές έχουν παρατηρήσει ότι η χρυσή αναλογία είναι εκφρασμένη σε όστρακα θαλάσσιων οργανισμών, στη διάταξη των κλαδιών, ανάμεσα στους μίσχους των φυτών και τις φλέβες στα φύλλα καθώς και στους σκελετούς των ζώων και των ανθρώπων, στις διακλαδώσεις των φλεβών και των νεύρων τους, σε αναλογίες χημικών ενώσεων και τη γεωμετρία των κρυστάλλων. Ορισμένοι μάλιστα έχουν προτείνει συνδέσεις μεταξύ της χρυσής αναλογίας και του ανθρώπινου DNA.
Στη μεγαλύτερη δυνατή κλίμακα εμφανίζεται στο σχήμα των σπειροειδών γαλαξιών, τεράστιων σχηματισμών από εκατοντάδες δισεκατομμύρια αστέρια.
Κατασκευή ορθογωνίου με πλευρές φ και 1:
1. Κατασκευάζουμε τετράγωνο πλευράς 1.
2. Φέρουμε ευθεία παράλληλη προς τη μια βάση και χωρίζουμε το τετράγωνο σε δύο ίσα ορθογώνια (πλευρών 1 και 1/2) και φέρνουμε μία διαγώνιο.
3. Κατασκευάζουμε κύκλο με κέντρο το μέσο της μίας πλευράς του τετραγώνου και ακτίνα τη διαγώνιο του ορθογωνίου.
4. Προεκτείνουμε την πλευρά του τετραγώνου στην οποία έχουμε ορίσει το κέντρο του κύκλου έως το σημείο του κύκλου που τελειώνει η διάμετρος
Το ευθύγραμμο τμήμα που αποτελείται από την πλευρά του τετραγώνου μαζί με την προέκταση έχει μήκος φ.
