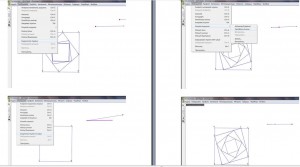
Η κατασκευή της σπείρας Baravelle
Φανταστείτε τώρα ότι βρισκόμαστε πάνω σε μια κυκλική πλατφόρμα και προχωράμε ευθύγραμμα από το κέντρο προς την περιφέρεια του κύκλου. Η καμπύλη που σχηματίζουμε είναι μια σπείρα. Ο Αρχιμήδης ασχολήθηκε με τη σπείρα αυτή, που είναι γνωστή με το όνομά του στο σύγγραμμά του Περί ελίκων. Οι δραστηριότητες που αφορούν τις σπείρες Baravelle έγιναν γνωστές μέσω του Choppin, J. M. (1994) στο άρθρο του Spiral through recursion (Σπείρες μέσω αναδρομής), που περιέχεται στο περιοδικό Mathematics Teacher του Εθνικού Συμβουλίου Δασκάλων των Μαθηματικών στις Ηνωμένες Πολιτείες (NCTM).
Στη συνέχεια παρουσιάζεται η κατασκευή μιας σπείρας Baravelle με διαδοχικές εικόνες
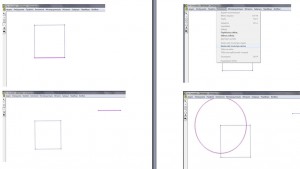
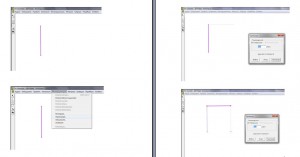
Στις εικόνες επάνω παρουσιάζεται πώς κατασκευάζουμε αρχικά ένα τετράγωνο.
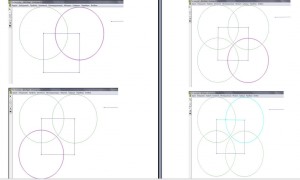
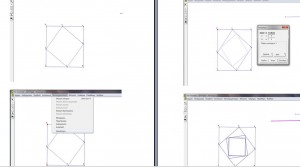
Στη συνέχεια πώς κατασκευάζουμε ένα τετράγωνο στο εσωτερικό του σχήματος ,κατασκευάζοντας ίσα τμήματα στο αρχικό τετράγωνο.
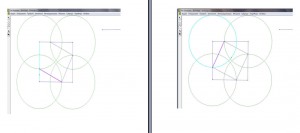
Στις εικόνες που ακολουθούν παρουσιάζεται πώς κατασκευάζουμε τη σπέιρα στο εσωτερικό και της δίνουμε κίνηση
Οι δραστηριότητες αυτές –που αφορούν σπείρες Baravelle– μπορούν να χρησιμοποιηθούν για την εισαγωγή της έννοιας της ακολουθίας, αλλά και του αθροίσματος άπειρων όρων φθίνουσας γεωμετρικής προόδου.
Διαβάστε περισσότερα για το θέμα στις παρακάτω δημοσιεύσεις :
https://www.academia.edu/3514387/_Baravell
Πατσιομίτου, Σ.(2006): Η σπείρα Baravelle. Ευκλείδης A΄. τ. 1. (61), 3-7.
https://www.academia.edu/3540476/_Baravelle_
Πατσιομίτου, Σ. (2008) Η κατασκευή της σπείρας Baravelle ως εργαλείο διαισθητικής κατανόησης αύξουσας και φθίνουσας ακολουθίας εμβαδών Πρακτικά 1ου Πανελληνίου Εκπαιδευτικού Συνεδρίου Ημαθίας,“Ψηφιακό Υλικό για την υποστήριξη του παιδαγωγικού έργου των εκπαιδευτικών” , σσ.316-324, Νάουσα, 9 – 11, Μαΐου 2008
Πατσιομίτου, Σ. (2010) Μαθαίνω Μαθηματικά με το Geometer’s Sketchpad v4 Εκδόσεις Κλειδάριθμος . Τόμος Β. ISBN 978-960-461-308
https://www.academia.edu/3610070/_Sierpinski-_Baravelle
https://www.academia.edu/3610059/_Baravelle_
Σχολιάστε
Για να σχολιάσετε πρέπει να συνδεθείτε.