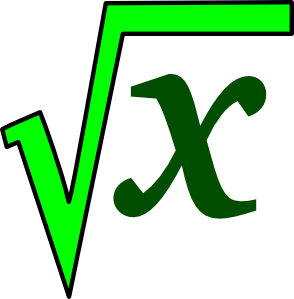Η λέξη ρίζα έχει πολλές σημασίες  σε διαφορετικούς τομείς, για παράδειγμα:

1. Στη βοτανική η λέξη ρίζα είναι το κάτω μέρος του φυτού που βρίσκεται μέσα στο έδαφος.
2. Στη οδοντιατρική ονομάζεται το κάτω μέρος του δοντιού που βρίσκεται μέσα στα ούλα.
3. Στη κομμωτική  ονομάζεται το κάτω μέρος της τρίχας που βρίσκεται μέσα στο δέρμα.
4. Στη χημεία ονομάζεται ομάδα ατόμων που δεν υφίσταται μεταβολή στη διάρκεια μιας χημικής αντίδρασης.
5. Στα μαθηματικά τετραγωνική ρίζα ονομάζουμε έναν (οποιοδήποτε) αριθμό που όταν υψωθεί στο τετράγωνο (δηλαδή πολλαπλασιαστεί με τον εαυτό του) μας δίνει το χ.

Για παράδειγμα η τετραγωνική ρίζα του 25 είναι ο αριθμός 5 επειδή 5Χ5=25 (5²=25 ή √25=5). Το ίδιο ισχύει και με την νιοστή ρίζα, δηλαδή η τετραγωνική ρίζα του χ είναι το α  ( α²=χ ή √_χ=α) . Ο συμβολισμός της τετραγωνικής ρίζας (√) άρχισε να χρησιμοποιείται το 1525 από τον Christoff Rudolf. Η τετραγωνική ρίζα ενός αριθμού α συμβολίζεται με :

• Το ριζικό ή σύμβολο της ρίζας (√) και Την υπόρριζη ποσότητα (α)

 

I. Ρίζες πραγματικών αριθμών

Αν α ≥ 0, η √_α  παριστάνει τη μη αρνητική λύση της εξίσωσης χ²= α . Είναι ο μη αρνητικός αριθμός  χ που όταν υψωθεί  στο τετράγωνο μας δίνει α.

II. Ιδιότητες τετραγωνικών ριζών:

√α² =│a│        √a  √β = √αβ         √α/√β = √α/β

III. Η Νιοστή ρίζα μη αρνητικού αριθμού:

Η ν-οστή ρίζα ( ν θετικός ακέραιος ) ενός μη αρνητικού αριθμού α συμβολίζεται ^ν√α και είναι ο μη αρνητικός αριθμός που, όταν υψωθεί στη ν δίνει α. Αν α ≥ 0, τότε η ^ω√α παριστάνει τη μη αρνητική  λύση της εξίσωσης χ^ν=α

IV. Ιδιότητες ριζών:

Αν α ≥ 0:

• (^ν√α)^ν = α και ^ν√α^ν= α
• ^ν√α  ^ν√β = ^ν√αβ ( Η ιδιότητα αυτή ισχύει και για περισσότερους  από δύο παράγοντες)
• ^ν√α/^ν√β  = ^ν√α/β  (β ≠ 0)
• ^μ√^ν√α = ^μν√α
• ^νρ√α^μρ =  ^ν√α^μ

Αν α,β ≥ Ο και κ θετικός ακέραιος, τότε:

^ν√α^κ = (^ν√α)^κ      και   ^ν√α^ν β = α^ν√β